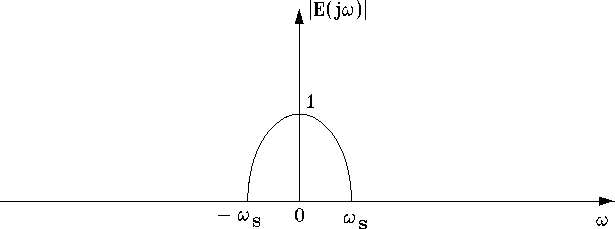
Figure 1.11: Possibile spettro di un segnale e(t) a banda limitata.

Al di sopra della pulsazione , lo spettro del segnale e(t) è nullo (cioè e(t) non contiene nessuna componente frequenziale).

Lo spettro del segnale campionato si ottiene dalla sostituendo jw al posto della variabile complessa s.

Nella Fig.  è riportato sia (b) l'andamento dello spettro del segnale campionato (nel caso in cui ) che (a) lo spettro del segnale da campionare.

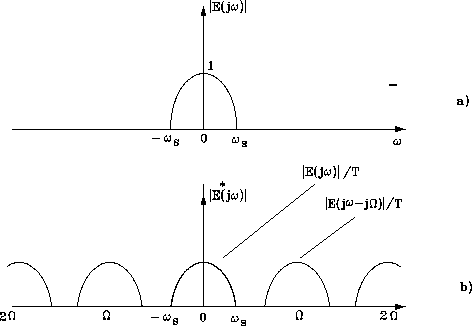
Figure 1.12: (a) Spettro del segnale da campionare e(t). (b) spettro del segnale campionato nel caso di

Nello spettro del segnale campionato la componenete |E(jw)|/T prende il nome di componente primaria, mentre tutte le altre componenti con prendono il nome di componenti complementari. È da sottolineare il fatto che la scelta di una pulsazione di campionamento tale che è essenziale in quanto tiene separate nello spettro le varie componenti che si presentano come la ripetizione della componente primaria.

Nel caso in cui la condizione non fosse rispettata il segnale campionato avrebbe uno spettro come quello riportato in Fig. 

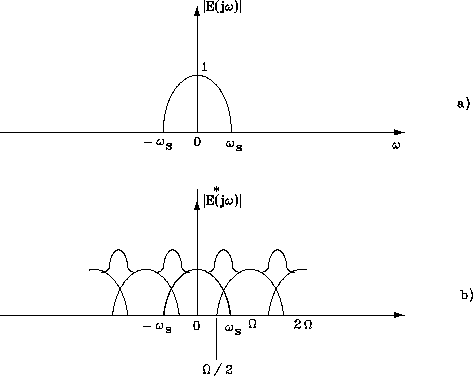
Figure 1.13: (a) Spettro del segnale da campionare e(t). (b) spettro del segnale campionato nel caso di

Le singole componenti spettrali (primaria e complementari) si sovrappongono parzialmente e si combinano per formare lo spettro risultante. Da quanto sopra, si deduce che se, e solo se la condizione è soddisfatta (Fig.  ), non si ha sovrapposizione ed è posibile distinguere la componente primaria da quelle complementari nel segnale campionato. In queste condizioni, se il segnale campionato viene mandato in ingresso ad un filtro ideale di spettro opportuno è possibile ricostruire il segnale originario e(t) a partire dal segnale a dati campionati.

Le considerazioni precedenti sono riassunte nel Teorema del campionamento o di Shannon:

In quanto segue si approfondisce il fenomeno legato al processo di campionamento quando le condizioni del teorema di Shannon non sono rispettate. Il fenomeno di sovrapposizione descritto in Fig.  prende il nome di aliasing. In altri termini l'aliasing corrisonde alla generazione (dopo l'operazione di campionamento) di nuove componenti spettrali nel range di frequenza della componente spettrale (primaria) di partenza.

Con riferimento alla Fig.  sia , una pulsazione compresa nel campo di pulsazioni in cui la componente primaria ed una componente complementare si sovrappongono. Per tale pulsazione esistono quindi sia un'armonica appartenente alla componente primaria che una ``nuova'' armonica appartenente alla componente complementare. In questo caso il segnale tempo-continuo ricostruito a partire dal segnale tempo-discreto per mezzo di un filtro passa-basso ideale non sarebbe in grado di ricostruire con fedeltà il segnale di partenza e(t). In particolare si perderebbero informazioni relative alle alte frequenze del segnale.

Una condizione necessaria per l'applicazione del Teorema di Shannon è che il segnale da campionare sia passa-basso. Considerazioni pratiche ci insegnano però che il segnale e(t) da campionare, anche per la presenza di disturbi (generalemente ad alta frequenza), ha una banda molto ampia se non infinita.

Per evitare il fernomeno dell'aliasing che sarebbe perciò inevitabile è quindi opportuno (pre-)filtrare il segnale e(t) prima del campionamento con un filtro anti-aliasing come descritto in Fig.  dove si è indicato con il segnale da campionare.

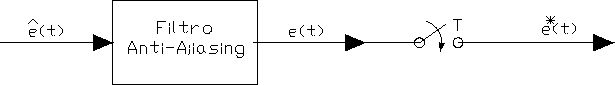
Figure 1.14: Filtro anti-aliasing.

Risultati soddisfacenti si ottengono con filtri passa-basso con sufficiente attenuazione (e.g. -40 db ed oltre) per