|
|
| |
CAPITOLO 8
CONCETTI SULLA REAZIONE
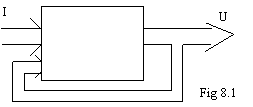
Consideriamo il
sistema di fig 8.1, con un ingresso e un'uscita; l'uscita viene riportata
tramite una anello all'ingresso e quindi va a sommarsi (o sottrarsi)
al 949b16j l'ingresso. In questo modo l'uscita contribuisce a modificare l'ingresso
e il nuovo ingresso produce una nuova uscita; si instaura quindi un anello di reazione.
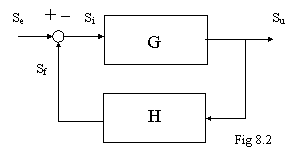
In fig. 8.2
compare la classica rappresentazione a blocchi di una reazione in cui il
blocco G trasforma l'ingresso in uscita e il blocco H riceve l'uscita e la
riporta al nodo di somma (sottrazione) presente all'ingresso. Facciamo ora
alcune assunzioni (peraltro temporanee): 1) Il sistema è
lineare 2) G e H sono
costanti e positivi
A seconda del segno, valgono queste due relazioni:
Si= Se + Sf Si = Se - Sf
In prima approssimazione possiamo associare mentalmente la somma al concetto di reazione positiva e la sottrazione al concetto di reazione negativa.
Definiamo la funzione di trasferimento ad anello chiuso o guadagno di anello chiuso il rapporto tra uscita e ingresso prima del nodo:
close loop gain GF
= ![]()
Definiamo guadagno di anello aperto il rapporto tra uscita e ingresso dopo il nodo:
open loop gain = ![]()
Nel caso particolare degli amplificatori, G rappresenta il guadagno dell'amplificatore base.
Vediamo di calcolare il guadagno di anello chiuso in funzione di G, nei due casi di nodo di somma e di sottrazione:
nodo di somma:
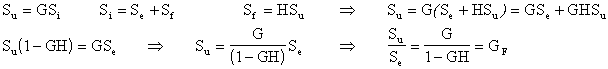
L'ultima espressione rappresenta il guadagno di anello chiuso espresso in funzione di G e H.
nodo di sottrazione:
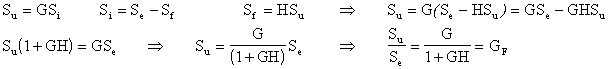
Nota bene: come vedremo, nei circuiti non è affatto semplice individuare i blocchi G e H, ma esiste un metodo per calcolare direttamente la quantità GH, che quindi risulta molto più importante dei singoli G e H.
Il blocco GH viene definito normalmente guadagno di anello.
Il guadagno di anello chiuso GF , nel caso della sottrazione, ha lo stesso segno di G ed è minore di G (viste le assunzioni fatte precedentemente).
Nel caso della somma, abbiamo tre sottocasi:
GH=1: teoricamente il guadagno è infinito (utilizzato negli oscillatori)
GH<1: GF > G e concorde in segno con G (utilizzato nei comparatori di soglia)
GH>1: l'uscita cambia segno ad ogni ciclo (sistema instabile)
Supponiamo ora di ragionare su una reazione con nodo di sottrazione.
Immaginiamo che Se rimanga costante e che ci sia una variazione positiva di Su; di conseguenza si ha una variazione positiva di Sf e dunque una variazione negativa di Si. Il risultato è intuitivo: la reazione negativa si oppone alle variazioni,cioè tende a stabilizzare il sistema perchè minimizza i cambiamenti dell'uscita. La reazione positiva, al contrario, tende ad esaltare le variazioni, ingigantendole.
Calcoliamo la variazione del guadagno di anello chiuso GF in rapporto alla variazione del guadagno G:

In altre parole, una variazione nel guadagno G induce una variazione di GF , ma divisa per la quantità (1+GH), quantità chiamata desensitivity. Questo significa che, come abbiamo già detto, nella reazione negativa una variazione di G ha un effetto molto trascurabile sul guadagno di anello chiuso (perché la quantità (1+GH) è normalmente grande, specialmente se parliamo di amplificatori).
Per fare un esempio, poniamo che il guadagno G possa variare da x a 10x, cioè dG/G=10, che siano G=25000 e H=0,1;
![]()
Si può vedere che più G è grande e meglio l'anello minimizza la variabilità di G. Quindi se abbiamo incertezza sul valore di G, ma G è abbastanza grande, otteniamo un valore di GF più piccolo ma ne conosciamo il valore con maggior precisione.
Vediamo ora la definizione vera e formale del guadagno di anello.
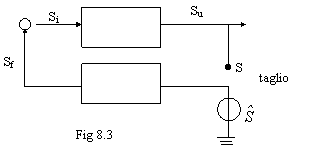
Dato un sistema ad
anello chiuso con Se=0, si definisce all'interno dell'anello un taglio, mantenendo invariati i livelli
di impedenza; si applica da un lato del taglio un generatore di tensione ![]() e si misura la tensione S all'altro lato del taglio (fig.
8.3).
e si misura la tensione S all'altro lato del taglio (fig.
8.3).
La definizione
che si trova in letteratura è la seguente: Ma noi
utilizzeremo la seguente definizione che differisce solo per il segno:
![]()
![]()
A questo punto siamo in grado di dare la vera definizione di reazione positiva e negativa:
una reazione è
positiva quando il rapporto S/![]() è positivo, è negativa quando tale rapporto è negativo.
è positivo, è negativa quando tale rapporto è negativo.
Come promesso, vediamo ora il metodo che si adotta per calcolare il guadagno di anello.
Consideriamo ad esempio il circuito di fig 8.4.
Passi: 1) Si elimina
il generatore indipendente 2) Si trasforma
il generatore dipendente in indipendente 3) Si calcola Vi (grandezza
pilotante) in funzione di

![]() .
.
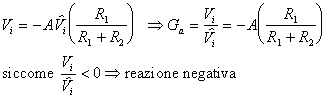
In questo esempio (amplificatore di tensione), A coincide con il blocco G e la parentesi coincide con il blocco H.
Se noi consideriamo invece l'amplificatore di trans-resistenza (identico al precedente ma il generatore di tensione si trova sul ramo con R1), otteniamo come guadagno di anello lo stesso valore, ma in questo caso non è vero che A coincide con G e la parentesi con H.
Comunque, come già detto, a noi non interessa individuare sul circuito i blocchi G e H, ma solo il metodo per calcolare Ga.
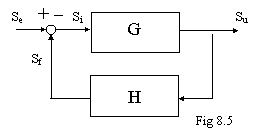
I concetti di reazione visti, ci interessano solo relativamente alla loro applicazione sugli amplificatori. Vediamo dunque più in dettaglio un anello di reazione quando esso rappresenta un amplificatore (fig 8.5).
Se=tensione, corrente o (raramente)
potenza Su=tensione, corrente, potenza G=amplificatore base H=blocco di reazione Si presentano
due problemi: 1) come
facciamo a prelevare la grandezza in uscita 2) come facciamo a sommare le grandezze in
ingresso
Supponiamo che i due blocchi siano dei doppi bipoli (fig 8.6).
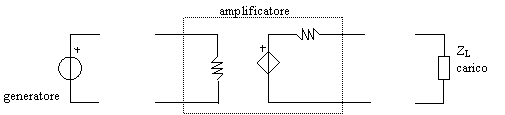
ipotesi: i blocchi sono monodirezionali
(nella realtà questo non è vero, ma qui ci semplifica le cose) Fig 8.6
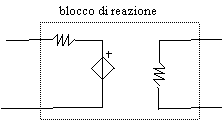
Nota: i due blocchi disegnati non devono avere per forza come funzioni di trasferimento i valori G e H, perché abbiamo già detto che negli amplificatori questi due blocchi sono difficilmente individuabili.
Cosa significa prelevare una tensione o una corrente? Significa misurare la tensione SUL carico e la corrente NEL carico. Infatti sono importanti queste grandezze solo se relative al carico, e non ad un qualche altro punto della reazione.
Leggere la tensione
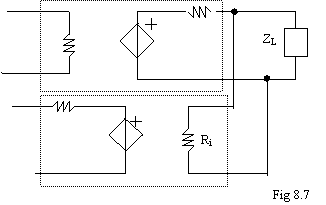
Per prelevare
la tensione sul carico metto l'ingresso del blocco H in PARALLELO al
carico (fig 8.7); questa operazione è valida indipendentemente dal fatto che il circuito sia rappresentato
tramite Thévenin o tramite Norton. In teoria la
resistenza in ingresso al blocco H (Ri) dovrebbe avere valore
infinito, cioè presentarsi come un circuito aperto, in modo da non
alterare la misura. In pratica
occorre che la resistenza abbia un valore molto alto.
Leggere la corrente
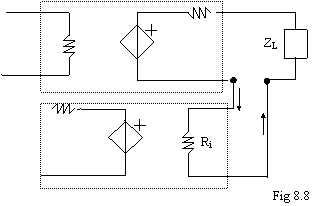
Per prelevare
la corrente nel carico metto l'ingresso del blocco H in SERIE con il carico
(fig 8.8); anche qui, l'operazione è valida indipendentemente dal fatto che il circuito sia rappresentato
tramite Thévenin o tramite Norton. Iin teoria la
resistenza in ingresso al blocco H (Ri) dovrebbe avere valore
nullo, cioè presentarsi come un circuito chiuso, in modo da non alterare la
misura.In pratica occorre che la resistenza abbia un valore molto piccolo.
Spostiamo la nostra attenzione sul punto di somma che si trova a sinistra dello schema a blocchi G-H. Circuitalmente, cosa significa sommare (sottrarre) correnti e tensioni? In linea generale, per sommare due tensioni occorre avere una maglia e una serie, per sommare due correnti occorre avere un nodo e un parallelo.
Sommare la tensione
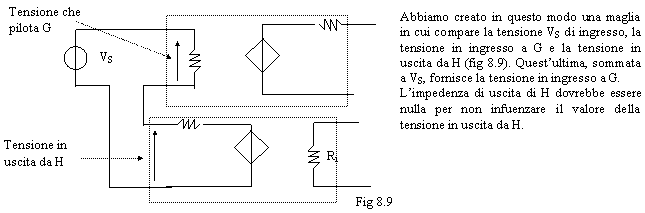
Sommare la corrente
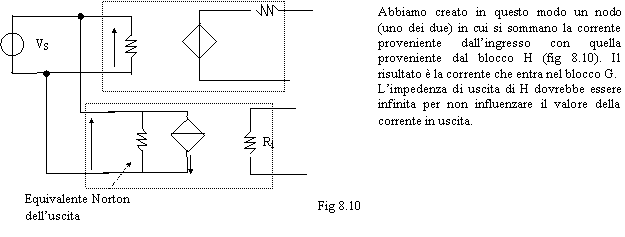
Abbiamo visto due configurazioni all'uscita (prelievo di tensione e di corrente) e due configurazioni all'ingresso (somma di tensioni e di correnti); con le 4 configurazioni possibili che otteniamo possiamo realizzare i 4 tipi di amplificatori che abbiamo già visto.
Fig 8.11 Amplificatore
di tensione Regola: immagino di sostituire il carico con un circuito aperto: se
l'anello di reazione non si apre, in uscita si ha un prelievo di tensione,
se l'anello si apre, ho un prelievo di corrente (viceversa se immagino di
sostituire il carico con un corto circuito). In questo caso
(fig 8.11) l'anello di reazione non
si apre, quindi ho all'uscita un prelievo di tensione. All'ingresso ho
una somma di tensioni e la maglia è composta da Vd, da VS
e dalla tensione Vf su R1: Vd=Vs-Vf Questo tipo di
reazione viene chiamata REAZIONE TENSIONE-SERIE.
La prima parte del nome si riferisce alla grandezza prelevata in uscita
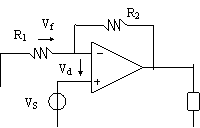 , la seconda parte alla grandezza sommata in ingresso (ricorda: somma
di tensione=serie, somma di
correnti=parallelo).
, la seconda parte alla grandezza sommata in ingresso (ricorda: somma
di tensione=serie, somma di
correnti=parallelo).
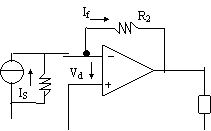
In riferimento
alla fig 8.12, in uscita viene prelevata una tensione (vale il discorso di
prima), mentre in ingresso vengono sommate delle correnti nel nodo
indicato. Questo tipo di
reazione si chiama REAZIONE TENSIONE-PARALLELO. Ii=Is-If
If In riferimento
alla fig 8.124,in uscita viene prelevata una corrente (vale il discorso
precedente); in ingresso sono sommate delle correnti nel nodo indicato. Questa reazione
prende il nome di REAZIONE CORRENTE-PARALLELO. Ii=Is-If Fig 8.14 Amplificatore
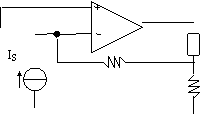
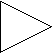
di corrente In riferimento
alla fig 8.13, in uscita viene prelevata una corrente (mettendo un circuito
aperto al posto del carico si apre l'anello di reazione); in ingresso si
sommano le tensioni VS , Vd e Vf . Questa
reazione prende il nome di REAZIONE CORRENTE-SERIE. Vd=Vs-Vf Fig 8.13 Amplificatore
di trans-conduttanza Fig 8.12 Amplificatore
di trans-resistenza Vf VS Vd
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Possiamo a questo punto dimostrare che le impedenze di ingresso e di uscita dei
4 amplificatori dipendendono dalla desensitivity.
Per far comparire questo termine nelle equazioni occorre scegliere
opportunamente il modello con cui rappresentiamo l'amplificatore di base.
Nei calcoli che seguono supponiamo che il blocco di reazione sia unidirezionale e che abbia impedenze di ingresso ideali (infinite o nulle a seconda dei casi).
Vi =VS - Vf (reazione negativa) R
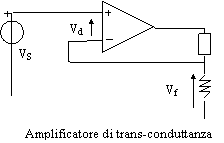
Fig 8.15
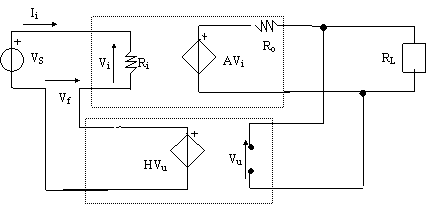
Impedenza di ingresso:

Impedenza di uscita:
per calcolarla, come al solito sostituisco il carico con un generatore di tensione V, annullo il generatore indipendente VS e poi determino il rapporto V/I:
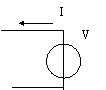
![]()
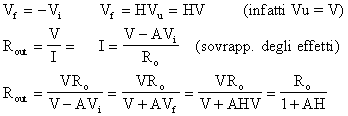
Sia l'impedenza di ingresso che quella di uscita dipendono da un fattore 1+AH che è la desensitivity.
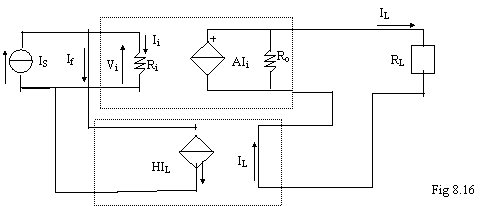
Impedenza di ingresso:
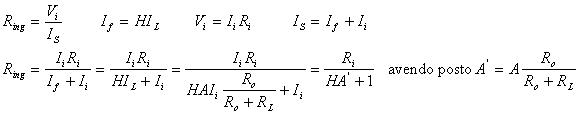
Impedenza di uscita:
per calcolarla, sostituisco il carico con un generatore di corrente e tolgo il generatore di corrente indipendente, poi calcolo il rapporto V/I:
![]()
![]()

Nota: come già detto prima di iniziare i calcoli, il blocco (1+AH) compare in
tutti i risultati non casualmente, ma grazie ad un'opportuna rappresentazione
del blocco amplificatore (tramite Thévenin o Norton).
Se provassimo a rifare i calcoli prendendo in esame una reazione positiva, nel caso in cui la quantità AH che compare nelle impedenze fosse minore di 1, troveremmo risultati analoghi ma opposti; se la quantità AH fosse invece maggiore di 1 otterremmo resistenze negative, e ciò significa semplicemente che il sistema sarebbe instabile (i poli si trovano nel semipiano positivo delle sigma) oppure oscillante.
Faremo alcuni calcoli "formali" e vedremo le differenze tra i risultati teorici e la realtà. Le regole della reazione servono durante la fase di progetto, non nel calcolo della rete, dove si utilizzano le regole dell'elettrotecnica.
Prendiamo in considerazione l'amplificatore di tensione e utilizziamo il metodo dei nodi.
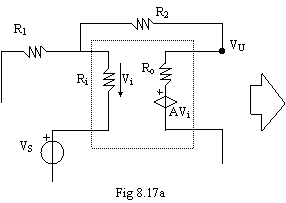
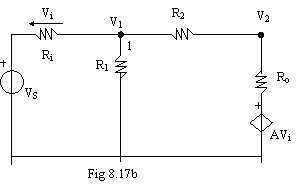

Le equazioni (1) e (2) formano un sistema con due incognite: VS e V2
. Utilizziamo il metodo di Kramer per calcolare V2:

Siccome V2 coincide con l'uscita VU , il rapporto trovato
rappresenta il guadagno GF dell'amplificatore di tensione; ora
modifichiamo un po' questa espressione in modo da far comparire una quantità di
tipo (1+XY); a questo scopo modifichiamo il denominatore:
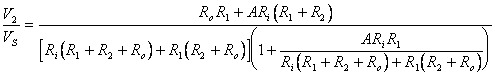
Riorganizziamo la seconda grande parentesi del denominatore:

 La
quantità che abbiamo messo infine in evidenza è riportata qui a sinistra.
La
quantità che abbiamo messo infine in evidenza è riportata qui a sinistra.
Questa quantità, a parte il segno che dipende dalla definizione scelta,
coincide con il guadagno di anello Ga.
Operiamo ancora una trasformazione al denominatore, questa volta sulla parentesi quadra a sinistra:

In questa forma possiamo mettere in evidenza due termini:

AD è detto guadagno del sistema "morto", cioè senza amplificatore; è come se avessimo messo a zero il generatore pilotato (Avi=0); in una reazione teorica questo implicherebbe annullare anche l'uscita, ma in un sistema reale i blocchi non sono unidirezionali e quindi un contributo di guadagno lo vediamo comunque. Tale contributo è tanto più trascurabile quanto è più grande il secondo termine AO , che dipende dal valore di A; siccome A negli amplificatori è un valore molto grande, il contributo di AD è effettivamente trascurabile rispetto ad AO.
AO rappresenta invece il guadagno dell'amplificatore di base (in altre parole il blocco G nello schema a blocchi).
Vale la seguente relazione:
![]()
Il guadagno ad anello aperto (AOL) è dato dalla somma del guadagno del sistema morto (senza amplificatore) con il guadagno intrinseco dell'amplificatore. Dividendo AOL per la quantità (1+Ga) si ottiene infine il guadagno ad anello chiuso.
![]()
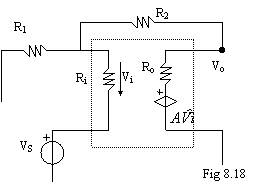
Prendiamo in considerazione il circuito appena studiato (fig 8.18).
L'ipotesi che facciamo è di considerare indipendente il generatore di
tensione dipendente. Individuiamo le variabili indipendenti e dipendenti di
questo sistema: variabili dipendenti: grandezza in uscita xo
(Vo) grand.
Di pilotaggio xi (Vi) variabili indipendenti: grandezza in ingresso xS
(VS) grandezza
pilotata
![]() (
(![]() )
)
![]()
Abbiamo espresso le variabili dipendenti in funzione di quelle indipendenti tramite opportuni coefficienti.
Ora ricaviamo ![]() dalla prima:
dalla prima:
![]()
Sostituiamo tale espressione nella seconda equazione e rinomianiamo le costanti:
![]()
Imponiamo ora l'equazione di vincolo: ![]() (infatti
circuitalmente la tensione pilotante e
quella pilotata hanno lo stesso valore); ora sostituiamo
(infatti
circuitalmente la tensione pilotante e
quella pilotata hanno lo stesso valore); ora sostituiamo![]() nella prima espressione del sistema :
nella prima espressione del sistema :

Quest'ultima espressione fornisce il rapporto tra uscita e ingresso, cioè il guadagno del sistema; nota la somiglianza di questa espressione con quella trovata nel caso di studio precedente.
La quantità t12 t22 è il guadagno di anello; invece, nel caso dell'amplificatore, la quantità t12 t 21 è il guadagno dell'amplificatore. Infine, t11 è il guadagno del sistema morto.
Calcoliamo i coefficienti tij :
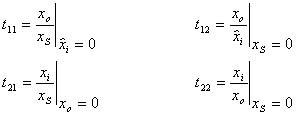
Applichiamo queste formule al circuito in esame:
t11:
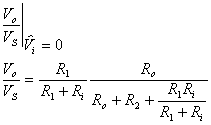
R1 R2 Ri Ro Vi VS Vo![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Questa quantità è il guadagno del sistema
morto AD
t12:
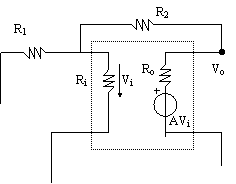
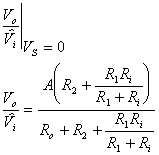
t21:
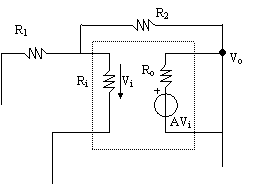
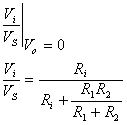
t22:
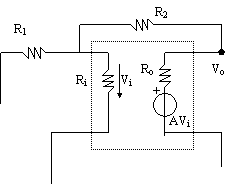

Nota: con questo metodo formale otteniamo gli stessi risultati che possiamo ottenere con i calcoli visti precedentemente.
La formula di Blackman è utile per calcolare l'impedenza di ingresso di un doppio bipolo reazionato.
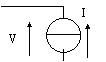
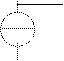
Per calcolare l'impedenza di ingresso di un doppio bipolo posso applicare ai morsetti di ingresso un generatore di tensione V, misurare la corrente I che eroga e calcolare il rapporto V/I (fig 8.19a). Oppure, al contrario, applico un generatore di corrente e trovo l'inverso dell'impedenza di ingresso calcolando il rapporto I/V (fig 8.19b).
Immaginando di
considerare una delle due grandezze come l'ingresso del sistema e l'altra
come l'uscita, V/I o I/V rappresentano le funzioni di trasferimento del
sistema: Fig 8.19a
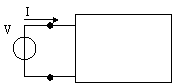
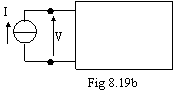
V=ingresso, I=uscita: I=f(V) I=ingresso, V=uscita: V=f(I)
Siccome parliamo di doppi bipoli reazionati, tale funzione avrà una forma di questo tipo (trovata precedentemente in via teorica):
![]()
Basandosi sulle considerazioni precedenti, la formula di Blackman permette di calcolare l'impedenza di ingresso:
![]()
dove RIF=impedenza di ingresso, RID=impedenza del sistema morto,
![]()
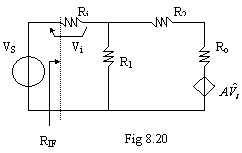
Per capire meglio, vediamo un esempio; consideriamo il circuito di fig 8.20.
RIF è l'impedenza vista dal
generatore di tensione VS, che rappresenta l'ingresso del
sistema. RID è l'impedenza vista da VS quando A=0.
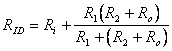
Per calcolare TOC sostituiamo l'ingresso VS con un circuito aperto (fig 8.21) e calcoliamo:
![]()
Per calcolare TSC sostituiamo
l'ingresso VS con un corto circuito (fig 8.22) e calcoliamo: quindi possiamo calcolare l'impedenza di
ingresso:

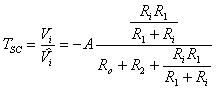

Allo stesso risultato si arriva calcolando l'impedenza di ingresso con i metodi "tradizionali".
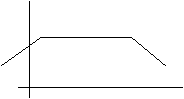
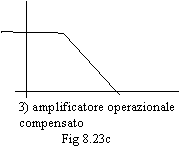
Vediamo la risposta in frequenza di tre amplificatori base quando vengono posti in reazione; i tre sono rappresentati in fig. 8.23a, 8.23b, 8.23c.

![]()
La funzione di trasferimento è
![]()
dove Go rappresenta l'altezza della parte piatta, a è il polo a minor frequenza e a è il polo a maggior frequenza.
Posso studiare l'effetto della reazione separando la zona di bassa frequenza e quella di alta frequenza.
Bassa frequenza:
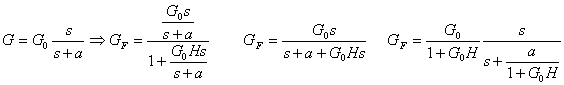
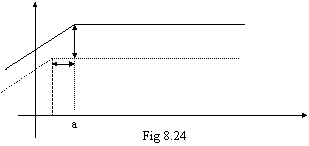
La curva di risposta si modifica: si
abbassa della quantità 1+G0H (diminuzione di guadagno) e il polo
si sposta verso lo zero della stessa quantità; lo zero invece non si sposta
(nella realtà si sposta poco). Lo spostamento è raffigurato in fig. 8.24.
Alta frequenza:
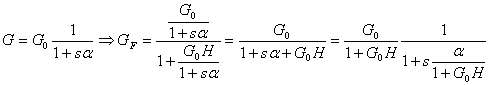
La curva di risposta si modifica: si
abbassa della quantità 1+G0H (diminuzione di guadagno) e il polo
si sposta verso infinito della stessa quantità (fig 8.25).
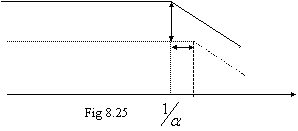
L'effetto complessivo consiste in una diminuzione del guadagno e in un allargamento della banda.
L'amplificatore operazionale compensato internamente presenta due poli, quindi è un sistema del secondo ordine (fig 8.26).

Poniamo che un sistema di questo tipo venga chiuso in un anello di reazione (con blocco di reazione costante):

Come si può vedere, la relazione che esprime il guadagno di anello chiuso è composta da una prima parte che indica l'abbassamento di guadagno per la solita quantità 1+G0H, e da una seconda parte che presenta due poli, che possono essere complessi coniugati o reali.
Il denominatore di questa seconda parte può essere scritto in altre due forme:
![]()
dove Q è detto fattore di qualità e k fattore di smorzamento.
Si può dimostrare che:
per ![]() presenta un massimo e
ha soluzioni complesse e coniugate
presenta un massimo e
ha soluzioni complesse e coniugate
per k>1 ha soluzioni reali
per ![]() ha due soluzioni
complesse e coniugate ma non presenta un massimo
ha due soluzioni
complesse e coniugate ma non presenta un massimo
Un caso particolare ma molto importante è il seguente.
Assumiamo che valga la seguente relazione:
![]() [
[![]() ]
]
cioè assumiamo che la distanza tra i due poli coincida con il guadagno di anello in bassa frequenza.
Riprendiamo la formula di prima aggiungendovi questa condizione:
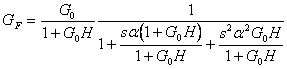
ipotizzando che ![]() , la formula precedente si semplifica:
, la formula precedente si semplifica:
![]() oppure
oppure 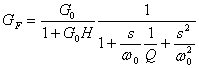
dove ![]() è la frequenza di
oscillazione non smorzata. Il polo più a destra ha la stessa pulsazione della
frequenza di oscillazione non smorzata (questo è il polo "naturale"
dell'amplificatore operazionale, mentre l'altro è il polo compensato;(vediamo
più avanti come si compensa).
è la frequenza di
oscillazione non smorzata. Il polo più a destra ha la stessa pulsazione della
frequenza di oscillazione non smorzata (questo è il polo "naturale"
dell'amplificatore operazionale, mentre l'altro è il polo compensato;(vediamo
più avanti come si compensa).
Risultano:
![]()
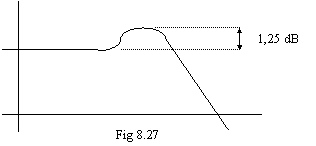
e siccome ![]() presenta un massimo
(fig 8.27).
presenta un massimo
(fig 8.27).
Riassumendo, sotto la condizione
![]() , realizziamo un anello chiuso con Q=1, k=1/2 e w a
, realizziamo un anello chiuso con Q=1, k=1/2 e w a
Se invece:
b>4aG0H ![]() presenta due soluzioni reali
presenta due soluzioni reali
b>=2aG0H ![]() presenta due soluzioni complesse coniugate ma non presenta un
massimo
presenta due soluzioni complesse coniugate ma non presenta un
massimo
b<2aG0H ![]() presenta due soluzioni complesse coniugate e un massimo
presenta due soluzioni complesse coniugate e un massimo
Un sistema del secondo ordine di questo tipo può essere realizzato anche tramite una rete simile a quella di fig 8.28.
Fig 8.28
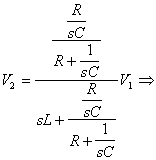
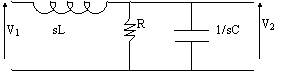
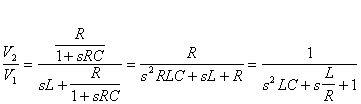
Abbiamo ottenuto una funzione di trasferimento del secondo ordine, molto simile a quella che abbiamo trovato precedentemente applicando un anello chiuso all'amplificatore compensato. Questo tipo di risultato è caratteristico di una rete LRC oppure di una rete RC chiusa in un anello di reazione.
Questo significa che tramite resistenze e condensatori posso realizzare gli stessi effetti di una rete contenente induttanze; le induttanze sono molto difficili da realizzare e da utilizzare, quindi questo risultato è molto importante.
CAPITOLO 8
SOMMARIO
8.1. Alcune definizioni.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .................
8.1.1. Definizione di guadagno di anello e di reazione positiva/negativa.......... ..... ...... .......... ..... ...... .....................
8.2 Amplificatori reazionati.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .........
8.2.1. Amplificatore di tensione.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ............................
8.2.2. Amplificatore di corrente.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .............................
8.3. CASO DI STUDIO: anello di reazione su amplificatore.......... ..... ...... .......... ..... ...... .......... ..... ...... .................
8.3.1. METODO GENERALE PER LA SOLUZIONE DI SISTEMI REAZIONATI CON 1 ANELLO.......... ..... ...... ......
8.3.2. FORMULA DI BLACKMAN (doppio bipolo reazionato).......... ..... ...... .......... ..... ...... .......... ..... ...... ...
8.4. Risposta in frequenza degli amplificatori reazionati.......... ..... ...... .......... ..... ...... .......... ..... ...... .....................
8.4.1. Amplificatore larga banda.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... .........................
8.4.2. Amplificatore operazionale.......... ..... ...... .......... ..... ...... .......... ..... ...... .......... ..... ...... ........................
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024