Il rapporto tra probabilità di ciascun intervallo Δx_i compreso in (a,b) per l'ampiezza dello stesso è costante e pari a

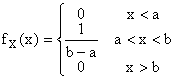 a<x<b

Tale rapporto costituisce la densità di probabilità della distribuzione uniforme su (a,b).

La probabilità di un qualunque intervallo (a,x) in (a,b) sarà data da

  a<x<b.

La funzione di distribuzione in x sarà

Rappresenta l'area sotto la curva f_X(x) con base (x-a) e al variare di x è la retta che congiunge i punti (a,0) e (b,1).

La funzione densità costante rappresenta il coefficiente angolare di tale retta.

Suddividiamo ora (a=x₀,b=x_n) in intervalli di ampiezza finita Δx_i=x_i+1-x_i , cui associamo una probabilita' finita p_i, tale che la somma delle probabilità di tutti gli intervalli sia pari a 1.

Nella ipotesi di distribuzione uniforme a tratti nei diversi intervalli Δx_i., possiamo definire in ciascuno di essi una densità di frequenza, pari al rapporto tra la probabilità associata all'intervallo e l'ampiezza dello stesso:

costante su ciascun intervallo, positiva e minore di 1.La probabilità su ciascuno degli intervalli potrà allora calcolarsi come nel caso precedente. La funzione di distribuzione sarà rettilinea a tratti e in ciascun tratto il coefficiente angolare della retta interessata è data dalla densità di probabilità del tratto stesso.

La funzione di distribuzione rappresenta l'area sotto la curva (costante a tratti) densità di probabilità.

Una distribuzione non uniforme può essere approssimata da una uniforme a tratti, su intervalli molto piccoli. Se facciamo tendere a zero l'ampiezza degliintervalli otteniamo una funzione densità continua, che rappresenta il coefficiente angolare della tangente alla corrispondente curva di distribuzione di probabilità anch'essa continua. Il legame tra funzione densità e funzione distribuzione diverranno:

 

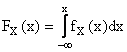
La probabilità di un intervallo finito (a,b) sarà data da

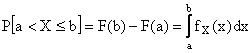
Si osservi che in tal caso la probabilità non cambia se l'intervallo comprende o meno gli estremi, in quanto questi hanno probabilità nulla.

Inoltre la probabilità di tutto l'insieme dei valori argomentali, che nel caso di variabile casuale continua può essere tutto l'asse sarà pari a 1:

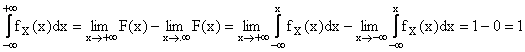
Tale proprietà viene detta condizione di normalizzazione.

La media di una distribuzione continua di probabilità

Riprendiamo il calcolo della media di una variabile casuale discreta, essa è data da:

Nel caso di variabile continua, possiamo calcolare la probabilità di intervalli (x_i,x_i+1) di ampiezza Δx_i , pari a

e possiamo scrivere, introducendo la densità costante di probabilità:

.

Una approssimazione della media può ottenersi dalla seguente espressione:

L'espressione esatta si ottiene facendo tendere a zero l'ampiezza degli intervalli Δx_i,

.

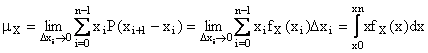Definiamo dunque l'operatore media per variabili continue, esso è dato da

,

dove gli estremi di integrazione sono quelli dell'intervallo in cui la variabile casuale assume valori.

La varianza di una variabile continua a una dimensione sarà dunque pari a

Trasformazioni di variabili casuali e teorema della media.

Estendiamo alle variabili continue, senza dimostrazione, quanto già visto per le variabili discrete

Data la trasformazione tra variabili mono-dimensionali

Y=g(X)

La densità di probabilità della variabile Y si ricava da quella della varibile X:

Il teorema della media diventa

esso consente di calcolare la media della variabile Y senza calcolarne la densità di probabilità.

Valgono le formule di propagazione della media e della varianza cosi' come nel caso discreto.

Esempio di variabile casuale monodimensionale continua: la distribuzione normale

Moltissimi fenomeni in natura seguono una legge normale. Un esempio sono i risultati di una misura di precisione. Si può supporre che alla misura 'reale' di una grandezza si aggiunga sempre un errore sistematico (costante e valutabile) e un errore accidentale dipendente da moltissimi fattori, dei quali tale errore è la somma. Questo errore ha una distribuzione normale.

Ma anche la distribuzione delle altezze di una popolazione può essere approssimata da una normale; si può pensare, infatti, che l'altezza sia il risultato di molti fattori: questioni ereditarie, standard alimentari della famiglia, fattori ambientali,etc.

Il teorema centrale della statistica garantisce che il comportamento di ogni fenomeno che possa pensarsi come la risulatnte di diversi fattori indipendenti, che ubbidiscono a modelli anche diversi da quello normale, sono approssimabili con una normale.

L'espressione della densità di probabilità di una normale è data da:

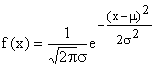
Il modello,sempre positivo e tale che l'area sottesa è pari a 1, dipende da due parametri  la media m e la varianza s . La radice della varianza, ovvero lo scarto quadratico medio rappresenta la distanza tra la media e il punto di flesso della curva.

La probabilità dei valori compresi nell'intervallo (m s m s), nel caso della distribuzione normale è pari al 99,7%, nell'intervallo (m s m s) è pari al 95%, nell'intervallo (m s m s) è pari al 68%.

Vediamo come utilizzare un tale modello per calcolare la probabilità di un certo intervallo di valori.

Tale probabilità è pari all'area sotto la curva normale con base pari all'intervallo che ci interessa. Tale area è il risulato di un integrale che non è calcolabile in maniera analitica. Il risultato dell'integrazione numerica è riportato nella tabella della normale ed è riferito ad una normale con media nulla e varianza unitaria, detta standard.

Il legame tra una normale con media e varianza date, che indichiamo con X, e una normale standardizzata, che indichiamo con Z, consiste in una traslazione e in una variazione di scala

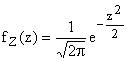
Se si vuole allora sapere la probabilita' che corrisponde ad un certo intervallo sotto la curva di media e varianze date, occorrera' trasformare tale intervallo nel corrispondente intervallo sotto la curva standardizzata. Se indichiamo con x₁ e x₂ gli estremi dell'intervallo della variabile X, l'intervallo corrispondente sotto la curva standardizzata sara' quello compreso tra gli estremi z₁ e z₂ ottenuti dalle seguenti relazioni:

    .

Bastera' allora leggere il valore di probabilita' relativo all'intervallo standard sulla tabella della Z e attribuirla all'intervallo corrispondente della X.