Trasmissione del calore

6.1 Introduzione

Lo scambio di energia tra due sistemi dovuto ad una differenza di temperature si dice che avviene per mezzo di un flusso di calore; questo scambio di energia avviene mediante un trasferimento di energia interna (o di entalpia) tra i due sistemi (sistemi che possono anche essere parti diverse dello stesso corpo): con il termine flusso di calore intendiamo il meccanismo di trasferimento, non la quantità trasferita.

E' d'uso corrente distinguere i vari processi di scambio termico i 434b17e n tre tipi o modi fondamentali sebbene sia piuttosto raro incontrare un problema di importanza pratica in cui non si verificano contemporaneamente almeno due di tali modi, se non tutti e tre.

A questi tre modi di scambio termico è stato dato il nome rispettivamente di conduzione, convezione e irraggiamento.

La conduzione del calore è il termine impiegato per descrivere il meccanismo di scambio di energia interna da un corpo ad un altro, o da una parte di un corpo ad un'altra parte dello stesso corpo, tramite lo scambio di energia cinetica legate al moto delle molecole, per collisione elastica nei fluidi e nei dielettirci e, nei metalli, essenzialmente per diffusione elettronica.

Questo flusso di energia o calore passa dal sistema molecolare a livello energetico più elevato a quello a livello più basso, cioè da una regione ad alta temperatura ad una regione a bassa temperatura.

La caratteristica distintiva della conduzione sta nel fatto che essa avviene  all'interno dei confini di un sistema o attraverso tali confini, nel caso di due sistemi posti a contatto, senza un apprezzabile spostamento di materia.

Secondo la teoria cinetica, la temperatura di un elemento di materia è proporzionale all'energia cinetica media delle molecole che lo costituiscono; l'energia posseduta da un elemento di materia in virtù della velocità e della posizione relativa delle molecole che lo costituiscono è stata a suo tempo chiamata energia interna: quanto maggiore è la velocità delle molecole, tanto maggiori risulteranno la temperatura e l'energia interna di un elemento di materia. Quando le molecole di una regione acquistano una energia cinetica media maggiore di quella delle molecole di una regione adiacente, circostanza resa evidente da una differenza nelle temperature, le molecole che posseggono l'energia maggiore trasmettono parte di questa energia alle molecole poste nella regione a temperatura minore; la conseguenza più evidente della conduzione termica è l'egualizzazione delle temperature.

Se si mantengono costanti le differenze di temperature aggiungendo e togliendo calore in punti opportuni, si riesce a realizzare un flusso continuo di calore dalla regione più calda a quella più fredda.

La convezione è un processo di trasporto di energia dovuto ad una azione combinata di con-

duzione termica, di immagazzinamento energetico e di moti di mescolamento; la convezione è in genere il meccanismo più importante che governa il trasferimento di energia tra una superficie solida e un liquido o un gas.

Il trasferimento di energia per convezione da una superficie la cui temperatura è più alta di quella del fluido circostante avviene secondo una successione di processi distinti. Si ha in primo luogo un flusso di calore per conduzione dalla superficie alle particelle di fluido immediatamente adiacenti alla superficie stessa: l'energia così trasferita serve ad aumentare la temperatura e l'energia interna di queste particelle di fluido. Quindi tali particelle si muovono verso una regione in cui il fluido si trova a temperatura più bassa e si mescolano ad esso trasmettendogli parte della propria energia: si ha quindi sia trasferimento di particelle che trasferimento di energia. L'energia è in realtà immagazzinata nelle particelle di fluido e viene trasportata grazie al loro moto di massa.

 Questo meccanismo non dipende, per la sua realizzazione, puramente da una differenza di tempreatura e perciò non è strettamente conforme alla definizione di flusso di calore. L'effetto finale, comunque. è quello di un traporto di energia, ed avviene nella direzione del gradiente di temperatura, pertanto è stato classificato come scambio termico per convezione.

Questo scambio termico si distingue ulteriormente  in  convezione libera  e convezione forzata, in base alla modalità secondo cui avviene il moto in seno alla massa fluida. Quando il moto di mescolamento avviene semplicemente come conseguenza di differenza di densità causate da un gradiente di temperatura, si parla di convezione naturale o libera; quando il moto di mescolamento è dovuto ad un 'azione esterna, per esempio quella di un ventilatore, si parla di convezione forzata.

L'irraggiamento è un processo durante il quale il calore fluisce da un corpo a temperatura più elevata ad un corpo a temperatura più bassa, senza che i due corpi siano posti a contatto.

L'irraggiamento ha luogo anche se tra i due corpi non è interposto alcun fluido, ossia ha luogo anche nel vuoto.

Il termine "irraggiamento" si applica in generale a tutti i fenomeni legati alla propagazione di onde elettromagnetiche; nel campo dello  scambio termico interessano soltanto quei fenomeni che si risolvono in un trasporto di energia attraverso un mezzo trasparente o nel vuoto in conseguenza di un certo valore della temperatura assunta da un corpo: l'energia trasmessa in questo modo prende il nome di calore radiante.

Tutti i corpi emettono calore radiante in modo continuo, e l'intensità dell'emissione dipende dalla natura e dalla temperatura della superficie emittente. L'energia radiante si propaga con la velocità della luce e ricorda fenomenologicamente la propagazione delle onde luminose: luce e irraggiamento termico differiscono solo per la lunghezza d'onda. Il calore radiante emesso da un corpo si propaga nello spazio con leggi desumibili dalla teoria ondulatoria: quando le onde di radiazione incontrano un altro corpo può verificarsi, in corrispondenza della superficie di tale corpo, una riflessione o un assorbimento dell'energia associata alle onde, energia che può essere interamente trattenuta dal corpo o parzialmente riemessa sotto forma di energia radiante, generalmente a lunghezza d'onda diversa.

Lo scambio termico per irraggiamento diventa sempre più importante al crescere della temperatura della superficie emittente; in parecchi problemi pratici, in cui sono interessati corpi con temperature prossime a quella ambiente il calore radiante può essere spesso trascurato.

6.2 Leggi fondamentali dello scambio termico

Quando esiste all'interno di un corpo un gradiente di temperatura l'esperienza ha mostrato che ha luogo un trasferimento di energia dalla temperatura più alta alla regione a temperatura più bassa: si può affermare che si ha trasferimento di energia per conduzione e che il flusso termico trasferito per unità di area è proporzionale al gradiente normale di temperatura. Consideriamo due superfici isoterme:

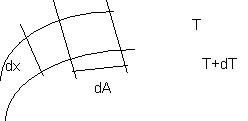
                                                               Figura 6. 1

Se individuiamo una direzione di propagazione normale a queste superfici il calore trasmesso nell'intervallo di tempo d  è:

                                                                     dQ = -KdA  

dove:

     K è una costante positiva chiamata conducibilità termica [W/m°C];

     dA è l'area normale alla direzione di propagazione;

     dx è lo spessore di materiale ai capi del quale c'è una  differenza di temperatura dT.

Il segno meno è stato inserito al fine di soddisfare il II principio della termodinamica, in modo cioè che il calore fluisca verso regioni a temperature inferiori.

Esprimiamo ora il flusso termico, cioè l'energia trasmessa nell'unità di tempo (Q)  . Si ottiene la legge di Fourier:

                                                                        = -K A

Vediamo ora di determinare l'espressione fondamentale che governa lo scambio termico in un solido, utilizzando la legge di Fourier come equazione di partenza.

Si consideri il sistema monodimensionale schematizzato in figura (6.2); se il sistema è in condizioni stazionarie, e cioè se la sua temperatura non varia in funzione del tempo, è sufficente integrare l'equazione di Fourier con le opportune condizioni  al contorno per conoscere il legame funzionale tra le variabili interessate.

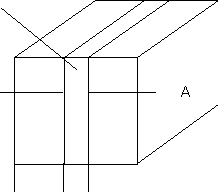
Figura 6. 2

Se invece il sistema non è in condizioni stazionarie, cioè se la sua temperatura varia in funzione del tempo,  e se inoltre sono presenti sorgenti  o pozzi di energia termica all'interno del solido, la situazione è più complessa.

Si consideri il caso generale con temperatura variabile nel tempo e con sorgenti di calore presenti all'interno del corpo: per l'elemento di volume schematizzato in figura, di area trasversale A e di spessore dx, occorre scrivere un'equazione di bilancio tra tutte le energie termiche che, nell'unità di tempo, interessano l'elemento stesso.

Si potrà scrivere cioè che la somma del flusso termico entrante per conduzione dalla faccia di sinistra e del flusso termico generato all'interno dell'elemento deve essere uguale alla somma della variazione dell'energia interna dell'elemento nell'unità di tempo e del flusso termico che esce per conduzione dalla faccia destra.

Il flusso entrante per conduzione dalla faccia di sinistra è:

                                                                     

Il flusso generato all'interno dell'elemento di volume è:

                                                                       

dove q è l'energia generata nell'unità di tempo per ogni unità di volume dell'elemento.

La variazione nell'unità di tempo dell'energia interna dell'elemento di volume risulta:

                                                   

dove:

     è la densità del materiale costituente l'elemento di volume;

     c è il calore specifico.

Il flusso uscente per conduzione dalla faccia destra risulta:

                                                                    

L'equazione di bilancio precedente può quindi scriversi come:

                                                                _x + _gen =  + _x+dx

e quindi, in base alle relazioni prima scritte:

                               -KA + qAdx = cA - A

semplificando si ottiene:

                                                              + q = c

Questa espressione rappresenta l'equazione unidimensionale della conduzione termica.

Nel caso più generale, occorre effettuare un'equazione di bilancio relativa a tutti gli assi coordinati.

L'espressione risultante è:

                                + q = c

che rappresenta l'equazione tridimensionale della conduzione termica.

Se la conducibilità termica K può essere ritenuta costante, si ottiene:

                                             

con    diffusività termica del materiale.

Introducendo l'operatore di Laplace ²  si ottiene:

                                                                   =

quanto più grande è il valore di  , tanto più veloce sarà la diffusione del calore all'interno del materiale. Dall'analisi dell'espressione di   vediamo che se K cresce si ha altà velocità di trasferimento; mentre se c decresce significa che solo una piccola parte dell'energia che attraversa il materiale viene assorbita ed utilizzata per aumentare la temperatura, mentre la parte maggiore resta disponibile per essere ulteriormente trasferita verso altre regioni.

In molti problemi pratici si incontrano solo dei casi particolari dell'equazione generale prima ricavata. Ad esempio:

- senza generazione interna di calore si ha:

                                                                         ^2T =

detta spesso equazione del calore;

- in condizioni stazionarie:

                                                                        =  0

detta equazione di Poisson;

- in condizioni stazionarie e senza generazione interna di calore:

                                                                              ² T = 0

detta equazione di Laplace.

Nel caso unidimensionale l'equazione di Laplace diviene:

                                                                             = 0

e con generazione interna di calore:

                                                                        +  = 0

La conducibilità termica è una proprietà fisica che denota la facilità con cui in una certa sostanza avviene la trasmissione di energia per moto intermolecolare. Si è riscontrato sperimentalmente che K dipende da:

                  composizione chimica della sostanza;

                  fase (solida, liquida, o gassosa);

                  struttura cristallina se solido;

                  temperatura e pressione cui il sistema è sottoposto;

                  omogeneità o meno del materiale.

Valgono i seguenti valori di conducibilità termica:

               

Materiale	K [W/m °C]
Argento	418
Rame	387
Cloroformio	0.0066
Aria	0.0243
Acqua	0.559
Ferro	45 73

Tabella 6.1

Si può subito osservare l'ampio campo di variabiltà di K: infatti l'argento ha un valore di K circa 60000 volte quella del cloroformio.

In generale un solido è migliore conduttore di un liquido che è a sua volta migliore conduttore di un gas.

Il trasferimento di energia nei solidi metallici  avviene mediante tre mediante tre meccanismi:

      urti molecolari;

      moto vibratorio dell'edificio cristallino nel suo complesso;

      migrazione degli elettroni di valenza nella direzione delle temperature decrescenti.

E'quest'ultimo meccanismo che rende i metalli conduttori molto migliori degli altri solidi. Questi elettroni liberi spiegano anche la proporzionalità sperimentalmente osservata tra la conducibilità elettrica e quella termica dei metalli puri.

Per quanto riguarda la soluzione analiticà dell'equazione generale della conduzione termica esistono in letteratura numerosissime soluzioni analitiche, che sono però limitate a problemi di geometria semplice e a condizioni al contorno esprimibili in forma analitica.    

           

Problemi più complessi sono stati affrontati con l'ausilio dell'elaboratore e risolti con metodi numerici.

Consideriamo una parete piana omogenea, di spessore s, conducibilità K e area A, trascurando gli effetti di bordo, si ottiene una distribuzione lineare delle temperatura :

Figura 6. 3

Per questa parete valgono:

                                                           = 0            = cost₁

                                                                    = -KA = cost

                                                                     T = cost₁ x + cost₂

                                                                    = KA

Per una parete cilindrica monostrato di raggio interno r_i ed esterno r_e e lunghezza L si ha:

                                                                  

Figura 6. 4

consideriamo il flusso per il raggio generico r:

                                                                      = - K2r L  

                                                                      dT = - dr

da cui integrando:

                                                               

                                                                  T₁ - T₂ = ln

                                                                    = 2LK

Il profilo di temperature in questo caso ha in andamento logaritmico:

                                                                  T₁ - T = ln

                                                                  T = T₁ - ln

Figura 6. 5

Questo termine si applica a quel meccanismo di scambio termico che ha luogo in un fluido, per azione combinata della conduzione e del moto di mescolamento delle particelle del fluido stesso.

Consideriamo un fluido avente temperature T_f a contatto con una parete a temperature T_s maggiore di T_f. A causa della viscosità del fluido la velocità del fluido alla parete è zero: pertanto nello strato fluido a contatto con la parete si ha trasmissione di calore per pura conduzione.

L'entità di tale scambio dipende dal gradiente di temperatura nel fluido a parete. Il gradiente di temperatura è influenzato però dall'entità del trasporto di calore e massa nel fluido in movimento.

Pertanto una conoscenza del moto del fluido è richiesta al fine di valutare quantitativamente la convezione termica.

Consideriamo il caso più semplice di moto a contatto di una parete piana:

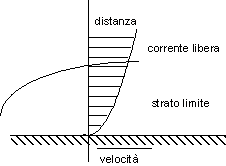
Figura 6. 6  - strato limite laminare

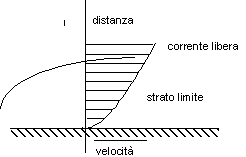
Figura 6. 7- strato limite turbolento

La velocità del fluido varierà da un valore detto di corrente libera, in punti lontani dalla parete, al valore zero in corrispondenza della parete stessa.

Per fluidi con bassi valori di viscosità, come l'aria e l'acqua, la regione adiacente alla superficie, in cui si hanno le massime variazioni di velocità, può essere anche molto sottile, in dipendenza della velocità di corrente libera.

Comunque, poichè il processo di convezione termica vicino alla parete è intimamente connesso con la conduzione termica ed il trasporto energetico dovuto al moto negli strati fluidi nell'immediata vicinanza della parete, non è possibile, nell'analisi di tale processo convettivo, prescindere dalla viscosità del fluido.

Poichè la regione in cui la viscosità del fluido gioca un ruolo predominante è costituta da uno strato molto sottile vicino alla parete si introduce il concetto di strato limite della velocità, definito come quel sottile strato di fluido in vicinanza della parete in cui si suppone siano importanti gli effetti viscosi.

Al di fuori dello  strato limite si può supporre che il fluido si muova come un fluido perfetto, a viscosità nulla.

All'interno dello strato limite il moto viscoso può essere sia laminare sia turbolento.

Nel caso di moto laminare dello strato limite, gli strati adiacenti di fluido scorrono l'uno sull'altro senza che vi sia mescolamento nella direzione normale ai filetti fluidi. In questo modo un'eventuale quantità di calore che fluisca dalla parete verso la corrente libera può farlo praticamente solo per conduzione.

Nel caso in cui il moto dello strato limite sia turbolento, il moto medio è essenzialmente parallelo alla superficie, ma ha sovrapposte delle componenti fluttuanti in direzione sia parallela sia normale alla superficie. Le fluttuazioni trasversali provocano un mescolamento addizionale del fluido che aumenta la velocità di trasporto dell'energia termica in direzione perpendicolare alla superficie.

Si hanno quindi due diversi profili di velocità nello strato limite, come schematizzato nella figure 6.6  e  6.7 .

Se la superficie solida è mantenuta ad una temperatura T_s diversa dalla temperatura T_f del fluido, misurata quest'ultima lontana dalla superficie, la variazione di temperatura del fluido è in qualche modo simile alla variazione di velocità, e cioè la variazione di temperatura, da T_s a T_f, è maggiormente concentrata in una regione adiacente alla parete.

Figura 6. 8

Si può pertanto definire uno strato limite termico come quella regione compresa tra la superficie ed il punto in cui la temperatura del fluido ha raggiunto il valore T_f.

Lo strato limite termico non coincide con quello della velocità, sebbene dipenda da esso.

La predizione del flusso termico di convezione richiede pertanto una comprensione completa dei principi della conduzione termica, della fluidodinamica e della teoria degli stati limite.

Tutte le complessità presenti in tale tentativo di soluzione analitica del problema sono normalmente concentrate in un unico parametro, introducendo la legge di raffreddamento di Newton:

                                                                      = h_c A (T_s - T_f)

cioè il flusso termico convettivo è proporzionale alla superficie di scambio ed alla differenza di temperatura tra parete e fluido, tramite un coefficente a cui si dà il nome di coefficente di scambio termico convettivo. Esso è dipende da:

                  tipo di fluido (aria, acqua,...) e sue proprietà fisiche;

                  tipo di moto del fluido (laminare/turbolento);

                  caratteristiche della superficie;

                  differenza di temperatura tra superficie e fluido.

Nel caso di convezione forzata (ad es. un ventilatore che soffia aria sopra una superficie che cede calore) il moto del fluido non è influenzato dallo scambio termico: la distribuzione di velocità e quella di temperatura possono quindi essere determinate indipendentemente, poichè il fenomeno fluidodinamico  e quello di scambio termico sono disaccoppiati.

Nel caso di convezione naturale, invece, i due fenomeni sono intimamente connessi, poichè il gradiente di densità che origina il moto dipende dal gradiente di temperatura che è causa anche dello scambio termico.

                                                          tabella 6.2 - valori tipici di h_c [W/m²K]

Le formule pratiche per il calcolo di h_c per numerose geometrie sono reperibili nei trattati di trasmissione del calore. In genere tali formule sono date come relazioni tra gruppi non dimensionali, come scaturisce dall'applicazione dell'analisi dimensionale al fenomeno della convezione.

Nel caso di convezione forzata si trova:   N_u = c

dove:

     N_u = h_cD/k = numero di Nusselt;

     R_e = cD/ = numero di Reynolds;

     P_r = c_p /k = numero di Prandl.

     c,m,n sono parametri determinati per via sperimentale. 

 

Nel caso invece di convezione naturale l'analisi dimensionale porta al risultato:

                                                                         N_u = c(G_r P_r)^m

dove:

     G_r = g ² (T_s - T_f)  = numero di Grashof;

     = coefficente di dilatazione del fluido; nel caso di gas  perfetto =1/T;

     g  = accelerazione di gravità.

Il termine irraggiamento definisce il trasporto di energia termica nella forma di radiazione elettromagnetica. Quando un flusso di energia raggiante incide su una superfice materiale esso viene in parte riflesso e in parte assorbito. Le frazioni assorbite, riflesse e trasmesse vengono individuate dai coefficenti di assorbimento  , riflessione  e trasmissione   per cui vale, per definizione, la relazione:

                                                                          + + = 1

Un corpo che assorbe tutta la radiazione incidente è detto corpo nero (per un corpo nero ovviamente ==0 e =1).

L'energia emessa da una superficie sotto forma di calore radiante dipende dalla temperatura assoluta e dalla natura della superficie stessa.

Il radiatore perfetto, o corpo nero, emette energia raggiante secondo la legge di Stefan - Boltzman:   

                                                                         

dove = 5.67 * 10^-8 W/m²K^4.

Questa legge stabilisce, che il flusso termico emesso per radiazione per unità di superficie emittente, è proporzionale alla quarta potenza della temperatura assoluta tramite la costante .

Mentre il fenomeno dell'emissione è indipendente dalle condizioni al contorno, affinchè si abbia scambio di energia termica raggiante tra due corpi diversi occorre in generale che tra due corpi esista una differenza di temperatura; se immaginiamo di avere un corpo nero che irradi in una cavità che lo circonda completamente e la cui superficie sia parimenti nera, cioè assorba tutta l'energia che incide su di essa, il valore netto del flusso termico scambiato vale naturalmente:

                                                                    = A₁

Avendo indicato con T₂ la temperatura assoluta della superficie di cavità.

La radiazione emessa da un corpo nero ha le seguenti proprietà:

      è isotropa, cioè è uniformemente distribuita spazialmente;

      rappresenta la massima radiazione che può essere emessa da un corpo ad una data temperatura.

I corpi reali non si comportano come radiatori ideali, ma emettono radiazioni con un'intensità minore di quella del corpo nero; se essi emettono, ad una temperatura uguale a quella del corpo nero, con uno spettro di emissione che per ogni lunghezza d'onda rappresenta una frazione costante dello spettro del corpo nero, vengono chiamati corpi grigi.

Si può in generale scrivere che il flusso di radiazione emesso da una superficie è:

                                                                        

dove  (minore di 1) è detta emissività della superficie. In generale è funzione della lunghezza d'onda della radiazione e della direzione di emissione. Per un corpo grigio   è costante.

In condizioni di equilibrio e per una data lunghezza d'onda l'emissività di una superficie è uguale al coefficente di assorbimento: =

Il valore netto del flusso termico scambiato tra un corpo grigio a temperatura T₁ ed una cavità nera a temperatura T₂ vale:       = A_{1 1}

L'emissività   del corpo grigio rappresenta il rapporto tra il flusso emesso da un corpo grigio e quello emesso da un corpo nero alla stessa temperatura.

Nel caso più generale, in cui entrambi i corpi siano grigi e in una situazione geometricamente più complessa di quella vista in precedenza, il flusso netto scambiato per radiazione termica si può esprimere con la relazione:

                                                              = F F_1,2 A₁

dove:

F     rappresenta una funzione dell'emissività prima definita;

F_1,2 è un fattore di forma geometrica che tiene conto della posizione geometrica relativa    delle superfici dei due corpi.   

La relazione sopra scritta risulta spesso scomoda nei calcoli, specialmente quando il corpo che si considera riceve o cede simultaneamente energia termica con processi diversi; è possibile scrivere:

                                                  = (T₁ + T₂ )(T₁ - T₂)

In condizioni ben individuate si potrà attribuire al prodotto  (T₁ - T₂)  un opportuno valore medio e quindi considerare  come funzione della differenza T₁ - T₂  e della superficie usando un coefficente di proporzionalità, detto di irraggiamento, che va calcolato caso per caso, con validità ristretta ad un certo intervallo di temperatura.

Si può ritenere valida la relazione:

                                                                     = h_i A₁ (T₁ - T₂)

avendo implicitamente definito il coefficente di scambio termico per irraggiamento hi definito da:

                                                         h_i = F F_1,2 (T₁ - T₂)

Si è così trasferito, come già nel caso del coefficente di scambio termico in un unico coefficente che va valutato volta per volta tenendo presenti tutte le condizioni al contorno del problema.

Se una parete è affacciata ad un ambiente contenente un fluido a temperatura diversa, il

fenomeno dello scambio termico è inevitabilmente complesso: la propagazione dell'energia avviene in parte per convezione e in parte per irraggiamento.

Siamo di fronte alla sovrapposizione di due fenomeni che obbediscono separatamente a leggi diverse; per i calcoli tecnici ci si serve abitualmente di espressioni semplificate. Si pone spesso:                      _tot = _i + _c

cioè la quantità totale di energia ceduta (o ricevuta) nell'unità di tempo è pari alla somma algebrica di quelle scambiate per irraggiamento (_i) e per convezione (_c).

Entrambe queste quantità si assumono come dipendenti dalla differenza di temperatura. Si scrive cioè:

                                   = _i + _c = h_i A (T₁ - T₂) + h_c A (T₁ - T₂) = h A (T₁ - T₂)

con:

                                                                            h = h_i + h_c

dove h assume il nome di coefficente di scambio termico liminare per la superficie A, somma di  h_i di irraggiamento e h_c di convezione.

Analogia elettrica

I problemi di scambio termico monodimensionale stazionario possono essere affrontati per mezzo della analogia elettrica che si basa sul fatto che le equazioni che descrivono lo scambio termico sono formalmente identiche alle leggi di Ohm.

Si può allora stabilire la seguente tabella di corrispondenze:

                                                                                          

Fenomeno termico	Fenomeno elettrico
Flusso di calore (W)	corrente I (A)
Differenza di temperatura T (K)	Tensione V (V)
- strato limite turbolento Resistenza termica R (K/W)	Resistenza elettrica R ()

                                                                            Tabella 6.3

Inoltre:

                                                                                         

La resistenza termica è definita in modi diversi.

     - strato pieno di area A, spessore s e condicibilità K:

                                                             = K A   R =

    - strato cilindrico di raggio interno r_i, raggio esterno r_e, conducibilità K e lunghezza L:

                                                        = 2 L K   R =

     - strato liminare piano:

                                                               = h S T    R =

     - strato liminare cilindrico:

                                                        = h 2 r L T   R =

L'analogia elettrica può essere utilizzata per studiare problemi di scambio termico in sistemi complessi, in presenza di resistenze termiche in serie e parallelo. Con le classiche formule dell'elettrotecnica si può determinare la resistenza globale R_g di una parete composta. Il reciproco della resistenza termica globale si chiama coefficente di scambio termico globale H_g della parete; esso rappresenta il flusso di calore scambiato attraverso la parete per una differenza di temperatura unitaria.