_{Il problema consiste nella determinazione dei coefficienti della sovrapposizione e degli autovalori nell'ambito di uno sviluppo perturbativo nel parametro l}

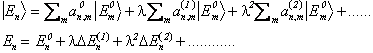
_{Sostituendo nella () ed eguagliando termini dello stesso ordine nel parametro perturbativo l si ottiengono le seguenti relazioni per i coefficienti a e per 151i87b le correzioni all'energia DE. Al primo ordine in l si ottiene.}

_{Dalla () otteniamo}

Proiettando su di un autostato di H₀ e sfruttando l'ortonormalità otteniamo

Gli autostati all'ordine zero di H coincidono con gli autostati di H_0.

Dalla relazione () valida al primo ordine primo ordine proiettando su un autostato di H₀ si ottiene

_{La ( ) esprime sia le correzioni in energia per n=k che i coefficienti a per n diverso da k.}

_{Senza perdere in generalità si può prendere il vettore che esprime la differenza tra un autostato della hamiltoniana perturbata ed il corrispondente di quella perturbata come ortogonale al primo a meno di termini del secondo ordine nella differenza . Vale infatti l'identità}

_{Trascurando il termine quadratico nella differenza degli autostati si ottiene}

_{La ( ) ci dice che la parte reale del prodotto scalare tra lo stato imperturbato e lo stato differenza è nullo. Ci si può a questo punto valere della possibilità di ridefinire lo stato differenza moltiplicandolo per un fattore di fase che renda nulla la parte immaginaria dello stesso prodotto scalare. Si realizza così la richiesta ortogonalità.}

_{Come esempio di applicazione del metodo consideriamo un oscillatore armonico perturbato da una barriera posta in x=0 di forma gaussiana}

 

_{La correzione in energia allo stato fondamentale risulta piccola rispetto all'energia dello stato fondamentale se}

_{Si noti come tale correzione si possa considerare piccola anche nel limite di una perturbazione di ampiezza che tende a zero. In tale limite la gaussiana g(x) diventa una delta di Dirac. Per quel che riguarda le correzioni allo stato.}

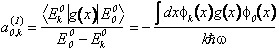
_{Data la parità della funzione d'onda dello stato fondamentale e della perturbazione g(x) saranno diverse da zero solo le correzioni relative a stati pari. Il calcolo esplicito si fa facilmente nel limite di perturbazione}

_{che coincide con una delta di Dirac.}

_{Si noti come la teoria delle perturbazioni dia in generale per lo stato una espressione in termini di una serie infinita. Ciò comporta delle difficoltà connesse alla convergenza della serie e alla valutazione dell'approssimazioni legate al troncamento della serie stessa.}

_{TEORIA DELLE PERTURBAZIONI IN PRESENZA DI DEGENERAZIONE}

_{Nel caso in cui l'autostato della Hamiltoniana imperturbata sia degenere, esista cioè almeno un'altra grandezza fisica S che commuta con l'Hamiltoniana imperturbata e ad uno stesso autovalore dell'energia corrispondano diversi autostati di S. Ad esempio nel caso del momento angolare se l' Hamiltoniana dipende solo dal modulo quadro di L ad uno stesso autostato dell'energia corrispondente all'autovalore l corrisponderanno diversi autostati della componente lungo l'asse z corrispondenti ai valori di m compresi tra -l e l . In tal caso dobbiamo usare come base per esprimere gli autostati e gli autovalori della hamiltoniana perturbata l'insieme degli autostati simutanei di H e di S .}

Sviluppando autostati ed autovalori nel parametro perturbativo l si ottiene analogamente al caso precedente

Se l'equazione agli autovalori deve essere soddisfatta ad ogni ordine nel parametro perturbativo l si ottiene

Proiettando su di un elemento della base e sfruttando l'ortonomalità si ricava

Gli autostati all'ordine zero di H coincidono con combinazioni lineari di elementi della base corrispondenti alla stessa energia.

Dalla relazione () valida al primo ordine proiettando su di un elemento della base otteniamo

_{Dalla ( ) otteniamo informazioni sulla correzione all'energia dai termini diagonali (n=r) e sulle correzioni allo stato da quelli non diagonali.}

_{La prima delle ( ) e' particolarmente interessante perche' si tratta di un sistema di Eqs omogenee per i coefficienti d'ordine zero che ha soluzione non identicamente nulla solo se e' nullo il determinante della matrice A}

Questa e' l'equazione che determina le correzioni all'energia . E' importante notare come anche i coefficienti d'ordine zero si determinino dalla ( ) e dalla condizione di normalizzazione. Nel limite di perturbazione nulla si raggiunge un particolare stato sovrapposizione corrispondente ad una certa energia tra tutti quelli possibili. La degenerazione del problema e' rimossa. L'eliminazione della degenerazione in teoria delle perturbazioni ha importanti conseguenze fisiche nei cosiddetti fenomeni di rottura spontanea di simmetria come vedremo nel seguito.

Come esempio consideriamo un sistema costituito da un sistema a due stati ed un oscillatore armonico. Il sistema a due livelli e' un modello per un sistema atomico, l'oscillatore per un modo di radiazione confinato in una cavita' .

Gli autostati sono autostati simultanei del sistema a due livelli e dell'oscillatore armonico

La degenerazione si ottiene nelle cosiddette condizioni di risonanza in cui la differenza di energia tra i due stati "atomici" e' pari ad un quanto di energia della "radiazione"

In condizioni di risonanza gli autostati sono degeneri a coppie eccetto lo stato fondamentale .

La perturbazione consiste in una energia associata all' accoppiamento tra il trasferimento tra uno stato all'altro del sistema atomico dato dall'operatore S_x e la deviazione dell'oscillatore dalla posizione di equilibrio.

Ripercorrendo nel caso particolare la procedura esposta precedentemente si utilizzano come base per ogni n gli elementi E₊(n-1) e E_-(n). L'autostato dell'energia dell'Hamiltoniana complessiva si potra' pertanto esprimere come segue

Sviluppando l'equazione agli autovalori fino al primo ordine nel parametro perturbativo l si ottengono

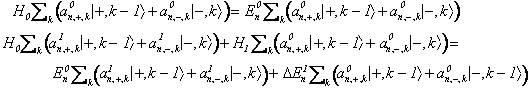
Proiettando su di un elemento della base di indici (-,r ) o (+,r-1) si ottiene dalla prima delle ( )

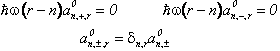
La stessa proiezione sulla seconda delle ( ) da' l'equazione per le correzioni in energia e per i coefficienti

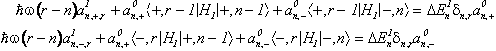
Per ogni n abbiamo un sistema di due equazioni in due incognite .L'equazione secolare che esprime la condizione per una soluzione non identicamente nulla e' la seguente

Tenendo conto della particolare scelta della hamiltoniana di perturbazione di ( ) si ottiene infine

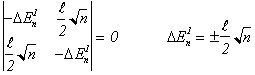
Tenendo conto della normalizzazione gli autostati dell'energia che si ottengono nel limite di perturbazione nulla sono per ogni n i seguenti due stati degeneri

La perturbazione ha rimosso la degenerazione.

Nota:La degenerazione e' legata all'esistenza di una simmetria, ovvero all'esistenza di un operatore hermitiano che commuta con l'Hamiltoniana. Tale simmetria puo' essere "accidentale" verificarsi cioe' solo per particolari valori dei parametri che compaiono nella Hamiltoniana, nel nostro caso possiamo definire un operatore di trasferimento di energia L tra l'oscillatore armonico ed il sistema a due livelli

Tale operatore trasforma un autostato dell'energia dell'Hamiltoniana H₀ in un autostato in cui l'atomo diminuisce di energia per effetto di una transizione dal livello superiore a quello inferiore e contemporaneamente la radiazione incrementa l'energia di un quanto o viceversa l'atomo assorbe energia con una transizione inversa e la radiazione cede un quanto. In condizioni risonanti l'energia totale non cambia per effetto del trasferimento dall'atomo alla radiazione o viceversa. E' facile verificare che solo in condizioni di risonanza l'operatore di trasferimento L commuta con l'Hamiltoniana. La verifica utilizza le seguenti relazioni di commutazione

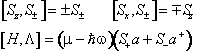
L'insieme degli stati degeneri si puo' ottenere applicando una trasformazione unitaria caratterizzata da un generatore L e da un parametro q. a due autostati degeneri indipendenti. E' facile infatti mostrare che lo stato che si ottiene da un autostato applicando la trasformazione unitaria associata all'operazione di simmetria e' autostato con lo stesso autovalore dell'energia. Se i due stati sono indipendenti,ovvero se il loro prodotto scalare e' nullo , tali saranno gli stati che si ottengono con la trasformazione unitaria. Nel nostro caso

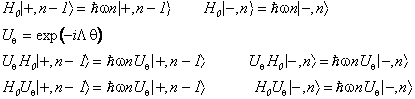
E' interessante esplicitare lo stato trasformato. Utilizzando le seguenti relazioni

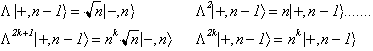
si ottiene che

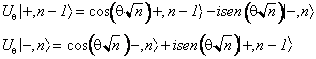
La rimozione della degenerazione porta a fissare l'anomalia q per ogni n al valore

METODO VARIAZIONALE

Si parte dalla identificazione di un insieme di stati che dipendono da uno o piu' parametri detti stati di prova e si cerca tra questi quello che meglio approssima lo stato fondamentale del sistema. Si puo' infatti mostrare che il valor medio su tali stati della Hamiltoniana del sistema e' sempre maggiore o al piu' eguale all'energia dello stato fondamentale. La dimostrazione si basa sull'ipotesi che gli stati di prova si possano esrimere come sovrapposizione di autostati dell'energia associati alla Hamiltoniana del sistema in considerazione.

Nella ( ) a rappresenta il parametro che identifica lo stato di prova. Possiamo calcolare il valor medio della Hamiltoniana e definire cosi' l'energia media nello stato di prova per ogni valore di a

Nel ricavare la ( ) si e' sfruttata l'ortonormalita' degli autostati.

Ponendo gli autostati in ordine di energia crescente con il numero quantico n e tenendo conto della normalizzazione degli stati di prova otteniamo quanto affermato

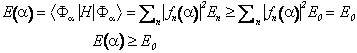
La migliore scelta corrispondera' pertanto al valore del parametro che rende minima l'energia media> Si noti che questa e' la migliore scelta all'interno di un certo insieme degli stati di prova caratterizzati dal suddetto parametro> Una scelta diffeente puo' migliorare o peggiorare l'approssimazione a seconda che il nuovo minimo sia minore o maggiore del precedente. Non esiste in generale un parametro di sviluppo atto a controllare l'approssimazione.

Consideriamo due semplici applicazioni. Nel primo caso consideriamo l'oscillatore armonico ed un insieme di funzioni d'onda di prova gaussiane normalizzate centrate sull'origine e di varianza a. L'energia nello stato di prova si calcola facilmente.

Il minimo si ottiene ponendo a zero la derivata dell'energia media rispetto al parametro.

Il risultato variazionale coincide con quello esatto infatti lo stato fondamentale appartiene all'insieme degli stati di prova.

Nel secondo caso consideriamo una particella in una doppia buca simmetrica rispetto all'origine. Il potenziale si puo' approssimare con due potenziali armonici centrati in a e -a che si racordano dolcemente con un potenziale costante al centro. Possiamo scegliere come funzione di prova una sovrapposizione con egual peso statistico di due stati che sono gli stati fondamentali relativi ai due oscillatori considerati separatamente> Il peso statistico eguale e' dovuto alla simmetria del problema. L'unico parametro da determinare e' quindi la fase relativa dei due stati.

Nella ( ) con 0,s e con 0,d intendiamo rispettivamente lo stato fondamentale dell'oscillatore armonico di destra o di sinistra. L'energia media sullo stato ( ) si esprime come somma di due termini l'uno legato al valor medio dell'energia che si ha se la particella si trova o a destra o a sinistra e l'altro dovuto al tunnelling ovvero alla sovrapposizione nella zona centrale delle ampiezze di probabilita' relative ai due minimi.

Nel ricavare la ( ) abbiamo fatto uso delle seguenti relazioni valide per la simmetria di H

L'energia totale sara' minima per a nullo se l'energia associata al tunnelling e' negativa. Tale energia si puo' valutare assumendo l'energia potenziale costante nella zona centrale ed integrando per parti il termine cinetico.

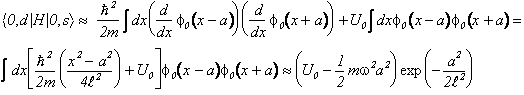
Se come abbiamo supposto il potenziale armonico approssima bene il potenziale della doppia buca fino alla zona di raccordo con una costante l'energia armonica deve risultare superiore al centro all'energia della barriera e pertanto il contributo del tunnelling deve essere negativo,

La correzione e' molto piccola se la distanza dal centro e' molto minore dell'incertezza associata allo stato fondamentale dell'oscillatore armonico. Lo stato ad energia superiore corrispondente alla combinazione antisimmetrica rimane normalmente molto al disotto dell'energia del primo stato eccitato dell'oscillatore armonico e puo' pertanto considerarsi come un nuovo stato eccitato ad energia molto vicina a quella dello stato fondamentale.

Possiamo ottenere il risultato considerando il limite in cui si ttrasura copletamente il tunneling. In tale limite la particella puo' essere osservata in uno dei due stati equivalenti associati ai due minimi> A ciascuno di tali stati compete la stessa energia . Si ha pertanto una degenerazione che viene rimossa dal tunnelling considerato come una perturbazione. Il risultato si generalizza al caso di un potenziale con un numero pari di buche equivalenti approssimate come potenziali armonici raccordati con barriere costanti. Se abbiamo N buche possiamo considerare uno stato di prova che dipendera' da N fattori di fase.

Lo stato 0,k denota lo stato fondamentale dell'oscillatore armonico che approssima la k-ma buca. Si noti che un fattore di fase e' ridondante. Il prefattore tiene conto della normalizzazione dello stato.

L'energia media sullo stato ( ) dipendera' da N parametri variazionali.

Nella doppia somma che appare in ( ) separiamo i termini diagonali che per simmetria sono tutti eguali e tra i termini non diagonali consideriamo solo quelli relativi a buche adiacenti. Trascuriamo cioe' la sovrapposizione di stati non adiacenti. Si ottiene cosi'

Si noti come nella ( ) gli stati corrispondenti agli indici 0,N+1 e 0,- 1 non esistano e debbano considerarsi come coincidenti con l'elemento neutro dello spazio vettoriale. Per simmetria i termini non diagonali sono tutti eguali.

La correzione in Energia dovuta all'hopping e' negativa per le stesse considerazioni fatte precedentemente. La condizione di minimo risulta pertanto

Lo stato di minima energia corrisponde alla combinazione lineare con differenza di fase nulla tra termini relativi a siti adiacenti. Gli stati ad energia superiore corrispondono a stati con una o più differenza di fase di p tra termini adiacenti. Si noti che per lo stato fondamentale la degenerazione è completamente rimossa dall'hopping mentre per gli stati eccitati occorre considerare la degenerazione legata ai possibili modi di scegliere la differenza di fase tra i diversi termini della combinazione lineare.

Definendo la densità degli stati come

I coefficienti di degenerazione g_n e le energie corrispondenti ai diversi stati si esprimono facilmente.

E' semplice calcolare la trasformata di Fourier della densità degli stati.

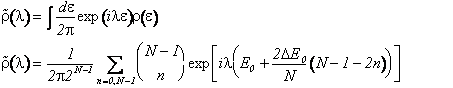
La somma si esegue facilmente con la formula dello sviluppo del binomio di Newton.

L'andamento della densità della trasformata di Fourier della densità degli stati è riportata in figura al variare di N. Per grandi N al primo ordine in 1/N si ottiene.

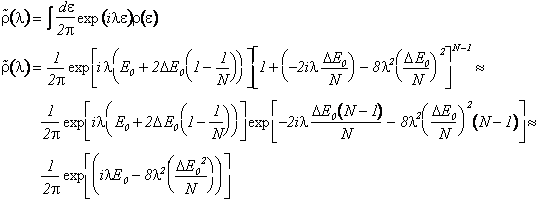
La ( ) è la trasformata di Fourier di una gaussiana centrata su E0 e di ampiezza