838j97i 838j97i   (1)

Valgono le usuali proprietà della somma e della moltiplicazione. Una _{caratteristica importante dello spazio vettoriale in esame è di essere} in generale uno spazio contenente un numero infinito di elementi. Si potranno pertanto costruire delle successioni e sotto opportune condizioni il sarà un elemento dello spazio vettoriale.

Esiste un prodotto scalare, esiste cioè una corrispondenza tra numeri complessi e coppie ordinate di elementi dello spazio. Dirac indica il prodetto scalare tra due elementi A,B con il simbolo "braket" (tale termine indica la parentesi in inglese)

838j97i 838j97i 838j97i 838j97i 838j97i   (2)

Valgono le usuali proprietà del prodotto scalare

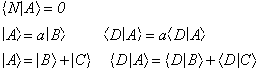838j97i 838j97i 838j97i (3)

Dirac individua il prodotto scalare come un prodotto tra un elemento dello spazio vettoriale dei Ket ed un elemento dello spazio "duale" dei Bra che indica con la parentesi angolare rovesciata . Ad ogni elemento dello spazio dei Ket corrisponde un elemento dello spazio dei Bra, alle operazioni di somma e moltiplicazione per un numero complesso c corrispondono la somma dei corrispondenti Bra e moltiplicazione per un numero complesso c* . Questa corrispondenza induce la struttura di spazio vettoriale allo spazio dei Bra. Conviene notare che l'unica operazione definita tra lo spazio dei ket e quello dei bra è il prodotto scalare. Una analogia può essere quella dello spazio vettoriale associato alle colonne (ket) e quello delle righe in cui si riportano i complessi coniugati degli stessi elementi considerati nelle colonne. Si possono definire la moltiplicazione per numeri complessi e la somma sia per le righe che per le colonne, si può associare un numero ad una coppia ordinata di colonne facendo il prodotto della riga corrispondente al secondo elemento per la colonna corrispondente al primo.

838j97i 838j97i (4)

Nello spazio vettoriale dei ket sono definiti gli operatori lineari come corrispondenze tra i ket che trasformano una combinazione lineare di ket nella stessa combinazione dei ket corrispondenti.

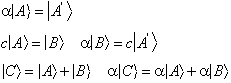838j97i 838j97i     (5)

Si definisce elemento di matrice di un operatore tra due stati A,B il prodotto scalare dello stato A' che l'operatore fa corrispondere ad a con lo stato B.

838j97i 838j97i 838j97i 838j97i     (6)

Un operatore è identificato dall'insieme dei suoi elementi di matrice. Hanno rilevanza fisica diretta gli elementi diagonali che definiscono, nel caso che l'operatoe sia una grandezza fisica, la media delle determinazioni di tale grandezza sullo stato A. Analogamente si può definire l'incertezza media. Più esplicitamente si suppone di poter eseguire un numero sufficientemente grande di misure indipendenti della grandezza in esame e di determinare così la media e l'incertezza. Per misure indipendenti intendiamo di disporre di tante realizzazioni equivalenti del nostro sistema fisico e di eseguire su ciascuna di esse una sola misura il cui risultato sia a_i. Si evita in tal modo che le misure risentano della perturbazione introdotta sul sistema da eventuali misure precedenti. Per realizzazioni indipendenti si intende che le condizioni di preparazione del sistema sono le stesse per ogni realizzazione.

838j97i 838j97i 838j97i 838j97i   (7)

I possibili risultati della misura della grandezza fisica a sono gli autovalori dell'operatore a . Infatti la misura riduce il sistema in uno stato in cui la grandezza è determnata (successive misure danno sempre lo stesso risultato). Questo implica che l'incertezza associata a tale stato sia nulla e ciò si realizza se lo stato dopo la misura è autostato di a. E' facile infatti mostrare come questa condizione sia sufficiente.

838j97i 838j97i 838j97i 838j97i (8)

La condizione è anche necessaria se la grandezza ha la l'importante proprietà di avere  un'insieme di autostati completo.. In termini fisici intendiamo che misure ripetute dela grandezza sono atte a ricostruire tutte le proprietà di un qualsiasi stato del nostro sistema. Ma ogni misura implica che lo stato si porti in un autostato per cui dalla conoscenza degli autostati e della frequenza con i corrispondenti autovalori sono osservati noi possiamo inferire delle prorprietà dello stato del sistema prima della misura.

Questo è quanto afferma il principio di sovrapposizione che nel presente formalismo possiamo così esprimere.

Se a_n sono i possibili autovalori della grandezza a (per semplicità li poniamo in corrispondenza con i numeri interi) ogni possibile stato del sistema fisico si esprime come combinazione lineare degli autostati di a. .

838j97i 838j97i 838j97i 838j97i (9)

La possibilità di esprimere un qualsiasi stato A come combinazione lineare di autostati corrisponde alla proprietà di tali stati di costituire una base per lo spazio vettoriale. Gli elementi di tale base corrispondono ai versori dello spazio vettoriale usuale.

E' conveniente porre tale base in forma ortonormale.

838j97i 838j97i 838j97i 838j97i 838j97i (10)

La completezza degli autostati di a ci consente di esprimere il valor medio e l'incertezza di a i un un qualsiasi stato.

838j97i 838j97i 838j97i    (11)

Nel ricavare la ( ) si è usata la proprietà di ortonormalità ( ). La ( ) ci consente di interpretare i coefficienti che intervengono nel principio di sovrapposizione come ampiezze di probabilità associate alla misura che dà come risultato a_n

Per l'incertezza otteniamo.

. 838j97i 838j97i   (12)

Si noti come per ricavare la ( ) si sia fatto uso della proprietà di normalizzazione dei coefficienti a di ( ).

Dalla ( ) otteniamo che condizione necessaria perché la grandezza fisica a sia nota senza incertezza sullo stato A e che questi coincida con uno degli autostati di a

I risultati di una misura fisica sono numeri reali, occorrerà pertanto che tali siano gli autovalori di a. Come nel caso dello spazio vettoriale costituito dalle funzioni d'onda dobbiamo introdurre la nozione di operatore hermitiano e dimostrare che condizione necessaria e sufficiente percé un operatore abbia autovalori reali è che questi sia hermitiano. Definiamo l'hermitiano coniugato tramite la seguente relazione tra gli elementi di matrice.

838j97i 838j97i 838j97i 838j97i (13)

Un operatore si dirà hermitiano se coincide con il suo hermitaiano coniugato.

Mostriamo che una grandezza fisica ( con ciò intendendo che si tratta di un operatore dotato di un insieme completo di autostati) deve corrispondere ad un operatore hermitiano.

Per questo è necessario mostrare che condizione necessaria e sufficiente perché gli autovalori della grandezza fisica siano reali è l'operatore corrispondente sia hermitiano.

Per la necessità occorre mostrare che se

838j97i 838j97i 838j97i    (14)

Se esprimiamo per la completezza sia A che B in termini di autostati di a ed utlizziamo la proprietà di ortonormalità ( ) si ottiene.

838j97i 838j97i    (15)

Se la ( ) deve essere soddisfatta per qualsiasi scelta degli stati A,B ovvero per qualsiasi scelta dei coefficienti a_n b_n, gli autovalori devono essere reali.

Per la sufficienza occorre mostrare

838j97i 838j97i (16)

Nella derivazione della ( ) si è fatto uso della proprietà degli operatori hermitiani coniugati

838j97i 838j97i     (17)

Nel caso in cui lo stato del sistema è definito più grandezze fisiche indipendenti tra di loro e misurabili con precisione indipendente diremo che l'insieme rappresentativo degli osservabili ( o grandezze fisiche) è costituito da un certo numero di operatori hermitiani indipendenti che ammettono un insieme completo di autostati simultanei.

In questo caso infatti la misura di una grandezza porta il sistema in un autostato dell'operatore corrispondente, operando poi la misura di una seconda grandezza, appartenente all'insieme rappresentativo, lo stato diviene autostato anche del secondo operatore. Devono cioé esistere autostati simultanei di tutti gli operatori dell'insieme rappreentativo e questi stati devono permettere di esprimere un qualsiasi stato del sistema.

Tramite questi autostati, cioè,si ricostruisce lo stato del sistema con il principio di sovrapposizione. Nel caso di un sistema rappresentativo costituito da due grandezze i cui autovalori siano in corrispondenza con i numeri interi,

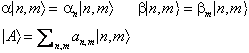838j97i 838j97i 838j97i    (18)

I coefficienti si interpretano come ampiezze di probabilità per l'osservazione di una coppia di autovalori.

In questo caso possiamo mostrare che condizione necessaria e sufficiente affinché due grandezze fisiche abbiano autostati in comune è che queste commutino tra di loro. La commutatività implica che le grandezze si possono misurare con precisione indipendente (la dimostrazione di questo punto si ricava immediatamente seguendo lo schema impiegato precedentemente)

La dimostrazione si ottiene con le seguenti considerazioni.

Necessità. Occorre mostrare che se due grandezze hanno in insieme completo di autostati comuni queste commutano. Consideriamo l'elemento di matrice del commutatore tra due stati qualsiasi ed espandiamo questi stati nella base degli autostati simultanei

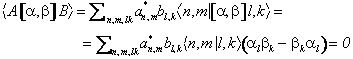838j97i 838j97i (19)

Essendo il risultato vero per qualsiasi elemento di matrice il commutatore deve essere nullo.

Sufficienza

Se due operatori a,b commutano, lo stato che si ottiene applicando k volte a all'autostato di b ancora autostato di b

838j97i 838j97i (20)

In generale (anche se a,b non commutano) l'autostato di b si potrà esprimere come combinazione lineare di autostati di a

838j97i 838j97i 838j97i 838j97i     (21)

In base alla precedente proprietà se a,b commutano è autostato anche una combinazione lineare del tipo

838j97i 838j97i 838j97i 838j97i     (22)

Questo è possibile solo se ciascuno degli autostati di a è anche autostato di b con lo stesso autovalore b_m

OPERATORI DI PROIEZONE

Il formalismo di Dirac consente di introdurre una particolare espressione per gli operatori di proiezione. Si dice operatore di proiezione sullo stato B l'operatore che applicato ad un qualsiasi stato A mi restituisce lo stato B moltiplicato per il prodotto scalare dello stato A per lo stato B.

838j97i 838j97i 838j97i 838j97i 838j97i (23)

Possiamo individuare l'operatore di proiezione come la sequenza di un Bra e di un Ket relativi allo stesso stato.

838j97i 838j97i 838j97i 838j97i 838j97i   (24)

Si tratta di un caso particolare di operatore definito come un bra A seguito da un Ket B. Nella analogia delle righe e delle colonne sitratta di un prodotto colonna per riga che definisce un operatore ovvero una matrice che agisce sulle colonne. Per due elementi A e B posso introdurre un operatore

838j97i 838j97i    (25)

La convenzione e' che applicando l'operatore ogni volta che appaiono di seguito nell'ordine un Bra ed un Ket si sostituisce il prodotto scalare corrispondente (Braket).

838j97i 838j97i 838j97i 838j97i (26)

L'hermitiano coniugato si ottiene facilmente scambiando l'ordine degli stati

838j97i 838j97i 838j97i 838j97i 838j97i (27)

La ( ) si dimostra facilmente utilizzando la detta convenzione

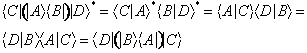838j97i 838j97i (28)

L'operatore di proiezione è pertanto un operatore hermitiano.

Sommando gli operatori di proiezione relativi ad un insieme completo di stati si ottiene l'operatore identità. Infatti vale la seguente relazione.

838j97i     (29)

Essendo lo stato A uno stato qualsiasi la somma sui proiettori è l'operatore identità.

838j97i 838j97i 838j97i 838j97i 838j97i (30)

A questo punto è necessaria una generalizzazione al caso di un insieme di stati autostati di una grandezza che assume valori che variano con continuita'. Ad esempio alla posizione. x saranno associati degli autostati tramite le seguente definizione.

838j97i 838j97i 838j97i 838j97i 838j97i     (31)

La generalizzazione naturale della rappresentazione dell'Identità sarà

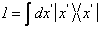838j97i 838j97i 838j97i 838j97i 838j97i     (32)

Applicando l'identita' data dalla ( ) ad un generico stato A si ottiene

838j97i 838j97i 838j97i    (33)

La funzione d'onda che caratterizza lo stato nella rappresentazione di Schrodinger corrisponde pertanto alla proiezione dello stato su di un autostato della posizione.

838j97i 838j97i 838j97i 838j97i 838j97i    (34)

Le diverse rappresentazioni del nostro sistema corrispondono a scelte diverse dell'operatore identità espresso ogni volta tramite autostati di diverse grandezze fisiche.

Esiste un problema ed è quello di riottenere lo stesso stato applicando l'identita' ad un autostato della posizione.

838j97i 838j97i 838j97i   (35)

Pe ottenere il risultato siamo costretti ad introdurre la cosiddetta proprità di ortonomalizzazione impropria degli autostati della posizione

838j97i 838j97i 838j97i 838j97i   (36)

Nonostante che la ( ) ponga dei severi problemi dal punto di vista di una formulazione matematicamente rigorosa della meccanica quantistica la definizione risulta estremamente efficace e come tale è accettata ed usata comunemente.

Un primo esempio è dato dalla trasformazione dell'elemento di matrice della posizione dal formalismo astratto a quello delle funzioni d'onda. Vogliamo cioe' mostrare che vale la seguente relazione.

838j97i 838j97i 838j97i     (37)

Per dimostrare la ( ) inseriamo due operatori identita' nell'elemento di matrice a sinistra della ( )

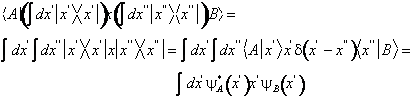838j97i   (38)

Per un qualsiasi operatore a l'elemento di matrice relativo a due stati si puo' esprimere nella rappresentazione degli autostati della posizione se sono noti gli elementi di matrice di a relativi a due qualsiasi autostati della posizione. Ripetendo infatti la procdura che ci ha portato a dimostrare la ( ) si ottiene.

838j97i 838j97i (39)

Tali elementi di matrice vanno determinati in base alle proprietà dell'operatore considerato. Nel caso della quantita' di moto possiamo assumere la proprieta' di commutazione e considerarne gli elementi di matrice tra autostati della posizione.

838j97i 838j97i 838j97i   (40)

Si ottiene cosí una relazione per gli elementi di matrice che ha per soluzione

838j97i 838j97i 838j97i 838j97i   (41)

La ( ) sodisfa la ( ) in senso come si dice debole la verifica va fatta cioe' moltiplicando a destra (o a sinistra) ambo i membri della ( ) per una funzione regolare dello spazio( funzione di prova) ed integrando. Se i due integrali danno lo stesso risultato indipendentemente dalla scelta della funzione di prova la relazione si dice soddisfatta in senso debole.

Utilizzando la ( ) si ottengono facilmente gli elementi di matrice della quantita' di moto nella rappresentazione di Scrodinger.

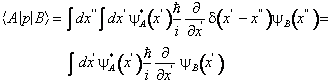838j97i 838j97i   (42)

Tutte le considerazioni fatte finora si riferiscono allo spazio vettoriale ad un certo istante. Se consideriamo l'evoluzione gli stati mutano al variare di un parametro tempo. La legge di evoluzione è ancora l'Equazione di Scrodinger generalizzata come segue.

838j97i 838j97i 838j97i 838j97i 838j97i (43)

Si noti che l'operazione di derivata rispetto al parametro tempo e' perfettamente definita. Nel nostro spazio vettoriale si puo' infatti costruire con le operazioni definite il rapporto incrementale e considerare quindi il limite che definisce la derivata

838j97i 838j97i 838j97i 838j97i (44)

Proiettando sugli autostati della posizione riotteniamo la formulazione originaria.

Prima di considerare la relazione tra diverse rappresentazioni di uno stesso stato illustriamo le proprieta' di un importante modello che si formula e si studia in modo elementare nello spazio astratto.

IL MODELLO A DUE STATI