F=0

L'equazione (1) diventa:

(1.1)

da cui, dopo una prima integrazione, si ottiene 

(costante)

e, dopo una seconda integrazione:

    (2.1)

Osserviamo che la soluzione x(t) è determinata se sono note le costanti v₀ e x₀, che rappresentano rispettivamente la velocità iniziale v₀ (che peraltro in questo caso è costante nel tempo) e la posizione iniziale x₀ (ovvero x(t=0)).

F=k (costante)

L'eqauzione (1) diventa:

(1.2)

Integrado successivamente come nel caso (1) si ottiene:

(2.2)

Di nuovo, la soluzione richiede la conoscenza delle costanti x₀ e v₀.

F=f(t)

La (1) diventa:

(1.3)

Da cui, integrando una prima volta:

e, integrando una seconda volta:

   (2.3)

Integrazione per  separazione di variabili

4.   con

Lequazione (1) diventa (1.4)

Posto

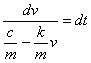
Questa equazione è integrabile direttamente perché a variabili separate. Con la condizione iniziale v=v₀ per t=0, si ottiene

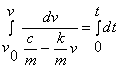
Passando agli esponenziali di ambo i membri dell'equazione e risolvendo rispetto a v(t) , nel caso v₀=0  si ricava

(2.4)

Per determinare x(t) si integra poi questa espressione per la v(t).

Integrazione mediante tentativi con funzioni di prova

5.

L'eq. (1) diventa  (1.5)

Questa è un'equazione differenziale lineare, omogenea, a coefficienti costanti, nella quale la funzione x e le sue derivate prima e seconda sono "poste sullo stesso piano", cioè la funzione soluzione deve essere tale che le sue derivate siano proporzionali alla funzione stessa. Ciò suggerisce di porre con A e a costanti da determinare.

Le derivate prima e seconda diventano allora

che, sostituite nell'equazione di partenza, danno

Dividendo per Aexp(at) si ottiene l'equazione algebrica di secondo grado

che ha soluzioni a a . Le soluzioni dell'equazione di partenza saranno quindi

, (2.5).

La costante A va ricavata dalle condizioni iniziali.

6. F=-kx

La (1) diventa

(1.6)

Anche questa è un'equazione differenziale lineare, omogenea, a coefficienti costanti, nella quale la funzione x e la sua derivata seconda sono "poste sullo stesso piano", cioè la funzione soluzione deve essere tale che la sua derivata seconda sia proporzionale alla funzione stessa. Ciò suggerisce di porre

   (2.6)

con A e j costanti da determinare.

La derivata seconda della x(t) è  

Sostituendo questa espressione nell'equazione di partenza, otteniamo

, equazione identicamente soddisfatta a patto di porre .

Per determinare le costanti A e si fa uso delle condizioni iniziali. Se ad esempio x(0)=x₀ e v(0)=0, si ha

,

che dà immediatamente e suggerisce di porre la soluzione nella forma

(3.1)

Se, viceversa, x(0)=0 e v(0)=v₀, si ha

,

che dà per le costanti i valori . La soluzione diventa dunque

    (3.2)