Trigonometria - Angoli & archi, Misura di angoli & archi

matematica

Angoli & archi

Si chiama angolo ciascuna delle due parti del piano in cui esso è diviso da due semirette uscenti da uno stesso punto O (incluse queste due semirette).

Si chiama arco la parte di circonferenza inclusa in un angolo al centro della circonferenza stessa.

Misura di angoli & archi

Per misurare un angolo occorre fissarne l'unità di misura. Un'unità spesso usata è il grado.
Si definisce il grado come la 360^ma parte dell'angolo giro. La 60^ma parte del grado si dice minuto primo e la 6^ma parte del minuto primo si dice minuto secondo.
In tutte le questioni di matematica superiore si impone tuttavia una misura degli angoli diversa da quella dei gradi e ben più comoda: viene presa come unità fondamentale non il grado bensì il radiante.
Si definisce angolo radiante l'angolo al centro di una circonferenza di raggio arbitrario, che sottende un arco di lunghezza eguale al raggio della circonferenza.

I fattori di conversione tra le due misure sono:
1 rad = 57°17'44"  & 929f53j nbsp;  180° = pi rad
D'ora in poi useremo quasi esclusivamente i radianti per cui si userà sempre pi moltiplicato per un determinato numero; ad esempio per dire 60°, scriveremo pi/3 (in quanto pi è 180°), o quando dovremo esprimere un angolo di 135°, scriveremo 3pi/4.

Anche per misurare gli archi occorre fissare un unità di misura. A tal scopo si assume come unità di misura l'arco il cui angolo al centro corrisponde all'unità di misura degli angoli. Così avremo:
l'arco grado, che è l'arco di circonferenza che corrisponde all'angolo al centro di un grado;
l'arco radiante, che è l'arco di circonferenza che corrisponde all'angolo al centro di un radiante.

La misura di un angolo orientato ^ABC la sua misura assoluta presa con il segno + o - a seconda che l'angolo ^AOB di positivo o negativo.
Se poi ^ABC è nullo, per definizione la sua misura è 0.

Seno & coseno

Sia data una circonferenza goniometrica: circonferenza di raggio unitario nel centro dell'origine. L'equazione di questa circonferenza è: X²+Y²=1
Consideriamo un qualsiasi angolo orientato A con il primo lato coincidente col semiasse positivo x. Sia P il punto di intersezione del secondo lato dell'angolo con la circonferenza.

Il seno e coseno sono delle grandezze che dipendono esclusivamente dall'angolo considerato.

Relazione fondamentale

La somma dei quadrati del seno e del coseno di uno stesso angolo orientato è uguale a 1.
Infatti P appartiene alla circonferenza goniometrica e soddisfa quindi l'equazione X²+Y²=1 ; il punto P è di coordinate (cos x, sin x) e quindi
P_x²+P_y²=1    ==>    (cos x)²+(sen x)²=1.
Ciò è dimostrabile anche dal Teorema di Pitagora: le misure di QP e OQ, che sono rispettivamente il seno e il coseno dell'angolo ^QOP, sono i cateti del triangolo rettangolo QOP la cui ipotenusa è uguale a 1 essendo il raggio unitario.

Tangente & cotangente

Esistono due definizioni di tangente di un angolo orientato. Noi partiremo dalla più usata per poi dimostrare la validità dell'altra definizione.

Riferendoci al primo dei due disegni, notiamo che i triangoli AOT e QOP sono simili, avendo entrambi un angolo retto, un angolo in comune e un angolo uguale. Si ha così la similitudine OA : TA = OQ : QP; essendo OA=1, TA=tg(^AOP), OQ=cos(^AOP), QP=sen(^AOP), si ha che: tg (^AOP) = cos (^AOP) : sen (^AOP) e possiamo concludere generalizzando che: tg x = sen x / cos x (Questa spesso viene considerata come la definizione di tangente).
Possiamo applicare un discorso analogo alla cotangente nel secondo disegno: per la similitudine dei triangoli POQ e TOB si ha che OT : BT = OP : QP e dunque sostituendo e generalizzando ctg x = cos x / sen x

Periodicità delle funzioni goniometriche

Le funzioni goniometriche sono delle funzioni periodiche, cioè restituiscono valori uguali per angoli che differiscono tra loro di uno o più periodi. Il seno e il coseno hanno un periodo di 2pi, cioé due angoli che differiscono di 2pi hanno lo stesso seno e coseno. Ad esempio 3/2 pi ha stesso seno e coseno di 7/2 pi, 11/2 pi e così via dicendo. Dal momento che 2pi equivale a 360°, possiamo anche dire che sen(14°)=sen(14°+360°)=sen(374°)=sen(734°)=ecc.. e lo stesso vale per il coseno.

La tangente e la cotangente hanno invece un periodo uguale a pi. Avendo quindi un periodo di 180°, possiamo ad esempio dire che tg(30°)=tg(210°)=tg(390°)=ecc. Possiamo vedere la cosa in maniera chiara nei grafici delle funzioni.

Grafico delle funzioni goniometriche

Grafico del seno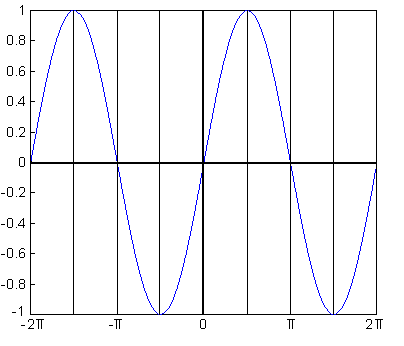

Con questo grafico si comprende bene la natura periodica del seno, come tutte le funzioni goniometriche. Si può notare come punti distanti tra loro di 2pi abbiano lo stesso seno. Il seno è una funzione dispari cioè sen(-a)=-sen(a). Il grafico di un seno viene chiamato sinusoide.

Grafico del coseno

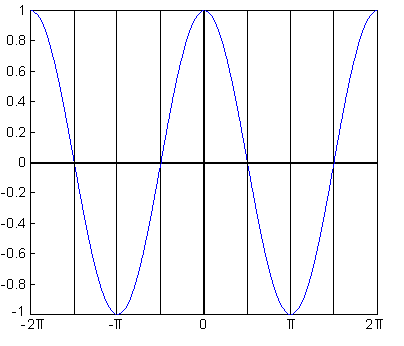
Anche nel coseno è palese la periodicità con modulo 2pi. E' inoltre riscontrabile che il coseno è una funzione pari cioè cos(-a)=cos(a).

Grafico della tangente

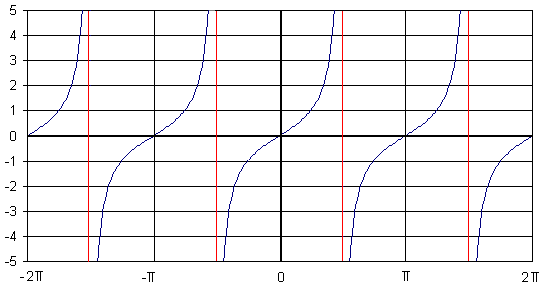
La tangente è una funzione ascendente fratta. Il fatto che sia ascendente è palese: in ogni punto la funzione tende a salire (Rigorosamente si deve dire che la retta tangente in ogni punto di questa funzione ha coefficiente angolare positivo, o ancor più rigorosamente che la derivata prima della tangente in ogni punto è positiva). Le rette verticali che passano a -3/2pi, a -pi/2, a pi/2 e a 3/2pi sono gli asintodi della funzione. La tangente quando si avvicina a quei valori tende a inf o a -inf. E' chiaro che essendo tg(x) = sen(x)/cos(x), la tangente non esiste quando cos(x)=0 e quindi nei punti in cui passano gli asintodi (le linee rosse, x = pi/2 + k pi). La tangente dunque non tocca mai gli asintodi se non all'infinito. La tangente è una funzione dispari.

Grafico della cotangente

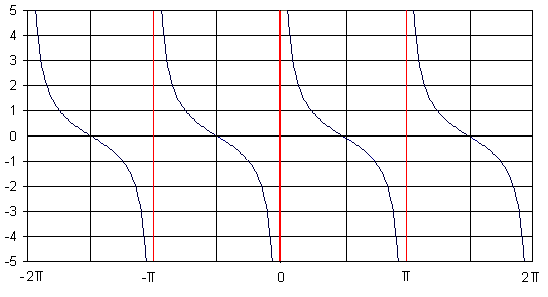
La cotangente è una funzione discendente fratta. Anche la cotangente è una funzione dispari. Essendo ctg(x)=cos(x)/sen(x), la cotangente non esiste quando il seno è nullo, quindi non tocca mai gli asintodi in x = k pi.

Segni e comportamenti delle funzioni goniometriche

Questa tabella indica il campo d'esistenza delle funzioni: sen(x) e cos(x) hanno significato sempre mentre invece per tg(x) e ctg(x), x deve essere diverso da alcuni valori che farebbero perdere significato alla funzione: per tg x, x deve essere diverso da (1+2k)pi/2 ossia deve avere un coseno diverso da zero; analogamente per ctg x, x deve essere diverso da quei valori che farebbero annullare il seno che sono k pi. Per quanto riduarda il codominio, il seno e il coseno variano tra -1 e 1 come tra l'altro i grafici fanno notare; per la tangente e la cotangente invece il codominio è infinito cioé la tangente o la cotangente di un angolo possono assumere qualsiasi valore.

Angoli notevoli

In genere il seno di un angolo è un numero irrazionale non esprimibile mediante un espressione finita tant'è che si ricorre all'approssimazione; per alcuni angoli tuttavia le funzioni goniometriche restituiscono risultati esprimibili mediante un'espressione più o meno semplice. Ecco qui un elenco di angoli notevoli.

Angoli associati

Se conosciamo il seno di un angolo A, possiamo calcolarci il valore del seno del complementare di A, del supplementare di A e di altri angoli che hanno qualche peculiarità con A. In questa tabella c'è una rapida trattazione di questi angoli.

Riduzione al primo quadrante e al primo ottante

Alla luce della tabella sopra esposta, possiamo calcolarci il seno di un angolo in maniera un pò più semplice, ecco un esempio:
sen(284°)=-sen(360°-284°)=-sen(76°)
ma sulla tavola dei logaritmi ci sono i valori dei seni che vanno da 0° a 45°. Ecco che siamo costretti ad operare un altro passaggio:
-sen(76°)=-cos(90°-76°)=-cos(24°)
con questo sistema in pratica si può calcolare il valore di una funzione goniometrica di un angolo qualsiasi, conoscendo i valori solo per gli angoli del primo ottante (da 0° a 45°).
Altri esempi:
tg(135°)=tg(180°-45°)=-tg(45°)=-1
cos(210°)=-cos(180°+30°)=-cos(30°)=-sqr(3)/2
ctg(300°)=-ctg(360°-60°)=-ctg(60°)=-tg(90°-30°)=-tg(30°)=-sqr(3)
E' importante quindi notare che tutti i valori finali sono delle espressioni basate su angoli appartenenti al primo ottante.

Espressione di tutte le funzioni goniometriche di un dato angolo orientato mediante una sola di esse

Commentiamo questa tabella.
Con questa tabella si può calcolare il valore di una funzione goniometrica di un angolo ^A a partire dal valore di un'altra funzione goniometrica; ad es.:
io so che sen x=0.6 e mi voglio calcolare coseno, tangente e cotangente dello stesso angolo. Alla tabella vedo che per esprimere il coseno mediante il seno si deve applicare l'espressione cos x = ±sqr(1-sen²x) e sostituendo sen x con 0.6 che è il valore che conosciamo otteniamo cos x = ±sqr(1-0.6²) = ±sqr(1-0.36) = ±sqr(0.64) = ±0.8
L'impossibilità di determinare il segno deriva dal fatto che non si conosce il quadrante a cui appartiene l'angolo. Infatti due angoli hanno seno 0.6 e questi possono avere coseno +0.8 e -0.8. Si procede analogamente per il calcolo della tangente: tg x = (sen x)/±sqr(1-sen²x) = 0.6/±sqr(1-0.6²) = 0.6/±sqr(0.64) = ±0.75
Per la verità già conoscevamo cos x e dunque avremmo potuto fare tg x = sen x/cos x.
Spero sia chiaro ora il significato della tabella ma ora vediamo di dimostrarne le varie espressioni.

Dimostrazione

Per la relazione fondamentale della trigonometria si ha che:
sen²x+cos²x=1 ==> sen²x=1-cos²x ==> sen x=±sqr(1-cos²x)
E per analogia:
sen²x+cos²x=1 ==> cos²x=1-sen²x ==> cos x=±sqr(1-sen²x)
Di qui sono chiare le espressioni di tg x e ctg x a partire da sen x e cos x. Prendiamo ad esempio tg x espresso mediante sen x:
tg x = (sen x)/(cos x) = (sen x)/±sqr(1-sen²x)

Passando alle espressioni di sen x e cos x a partire da tg x e ctg x.
sen²x = sen²x ==> (sen²x)/(sen²x+cos²x)=sen²x
Fin qui è chiaro? sen²x+cos²x è uguale a 1 per la relazione fondamentale della trigonometria. Ora divido numeratore e denominatore per cos²x e ottengo
(tg²x)/(1+tg²x) = sen²x ==> (tg x)/±sqr(1+tg²x) = sen x
E allo stesso modo:
cos²x = cos²x ==> (cos²x)/(sen²x+cos²x)=cos²x ==> 1/(1+tg²x) = cos²x ==> 1/±sqr(1+tg²x) = cos x
per la cotangente la dimostrazione è molto simile: basta dividere nel passaggio intermedio per sen²x invece che per cos²x.

Formule di sottrazione

DIMOSTRAZIONE

Per calcolare sen c si adotta questo procedimento: noi sappiamo che
sen c = cos (c-pi/2) = cos((b-a)-pi/2) = cos((b-pi/2)-a) =
applicando la formula di sottrazione del coseno...
sen c = cos(b-pi/2)*cos a + sen(b-pi/2)*sen a = (sen b)(cos a) - (cos b)(sen a)

Ecco il procedimento per calcolare tg (b-a)
tg c = (sen c)/(cos c) = ((sen b)(cos a) - (cos b)(sen a)) / ((cos b)(cos a) - (sen b)(sen a))
dividiamo ora numeratore e denominatore per (cos b)(cos a)...
tg c = ((tg b)-(tg a)) / (1 - (tg b)(tg a))

Infine ecco il procedimento per calcolare ctg (b-a)
ctg c = (cos c)/(sen c) = ((cos b)(cos a) + (sen b)(sen a)) / ((sen b)(cos a) - (cos b)(sen a))
dividiamo ora numeratore e denominatore per (sen b)(sen a)...
ctg c = ((ctg b)(ctg a) + 1) / ((ctg a)(ctg b))

Formule di addizione

DIMOSTRAZIONE

Le dimostrazioni sono banali in quanto basta utilizzare le formule di sottrazione con una lieve modifica:
cos(x+y) = cos(x-(-y)) = (cos x)(cos(-y)) + (sen x)(sen(-y)) = (cos x)(cos y) - (sen x)(sen y)

sen(x+y) = sen(x-(-y)) = (sen x)(cos(-y)) + (cos x)(sen(-y)) = (sen x)(cos y) + (cos x)(sen y)

tg(x+y) = tg(x-(-y)) = (tg x - tg(-y)) / (1 + (tg x)(tg(-y))) = (tg x+tg y)/(1-(tg x)(tg y))

ctg(x+y) = ctg(x-(-y)) = ((ctg x)(ctg(-y)) + 1) / (ctg(-y) - ctg x) = (-(ctg x)(ctg y)+1)/(-ctg y-ctg x) = ((ctg x)(ctg y)-1)/(ctg y+ctg x)

Formule di duplicazione

Anche in questo caso la dimostrazione è banale: basta utilizzare le formule di duplicazione:
cos(2x) = cos(x+x) = (cos x)(cos x) - (sen x)(sen x) = cos²x-sen²x

sen 2x) = sen(x+x) = (sen x)(cos x) + (sen x)(cos x) = 2(sen x)(cos x)

tg(2x) = tg(x+x) = (tg x + tg x)/(1-(tg x)(tg x)) = (2tg x)/(1-tg²x)

ctg 2x) = ctg(x+x) = ((ctg x)(ctg x)-1)/(ctg x + ctg x) = (ctg²x - 1)/(2ctg x)

Formule di bisezione

Queste formule si ricavano facilmente a partire dalle formule di duplicazione:
cos x = cos x ==> cos(2*x/2) = cos x ==> 2cos²(x/2)-1 = cos x ==> cos²(x/2) = (1+cos x)/2 ==> cos(x/2) = ±sqr((1+cos x)/2)

sen x/2) = ±sqr(1-cos²(x/2)) = ±sqr(1-((1+cos x)/2)) = ±sqr((1-cos x)/2)

tg x/2) = sen(x/2)/cos(x/2) = ±sqr((1-cos x)/2)/sqr((1+cos x)/2) = sqr((1-cos x)/(1+cos x))

ctg x/2) = 1/tg(x/2) = sqr((1+cos x)/(1-cos x))

Formule di Prostaferesi

Le formule di prostaferesi permettono di fattorizzare una somma di due seni o coseni. La dimostrazione è la seguente:
Sia p+q=x e p-q=y   segue che p=(x+y)/2 e q=(x-y)/2
sen x=(sen p)(cos q)+(sen q)(cos p)   sen y=(sen p)(cos q)-(sen q)(cos p)
cos x=(cos p)(cos q)-(sen p)(sen q)   cos y=(cos p)(cos q)+(sen p)(sen q)

sen x+sen y = 2(sen p)(cos q) = 2sen((x+y)/2)cos((x-y)/2)

sen x-sen y = 2(sen q)(cos p) = 2sen((x-y)/2)cos((x+y)/2)

cos x+cos y = 2(cos p)(cos q) = 2cos((x+y)/2)cos((x-y)/2)

cos x-cos y = -2(sen p)(sen q) = -2sen((x+y)/2)sen((x-y)/2)

Formule di Werner

Le formule di Werner svolgono praticamente l'opposto delle formule di prostaferesi
Anche in questo caso la dimostrazione di ognuna delle 3 formule è intuitiva...
Dalla formula di prostaferesi si ha che:

cos(x+y)-cos(x-y) = -2(sen x)(sen y) ==> (sen x)(sen y) = -1/2(cos(x+y)-cos(x-y)) = 1/2(cos(x-y)-cos(x+y))

cos(x+y)+cos(x-y) = 2(cos x)(cos y) ==> (cos x)(cos y) = 1/2(cos(x+y)+cos(x-y))

sen x+y)+sen(x-y) = 2(sen x)(cos y) ==> (sen x)(cos y) = 1/2(sen(x+y)+sen(x-y))

Formule parametriche in tg(x/2)

La dimostrazione per sen x è la seguente:
sen x = sen(2*x/2) = 2sen(x/2)cos(x/2)/1 = 2sen(x/2)cos(x/2)/(sen²(x/2)+cos²(x/2))
ora dividiamo tutto per cos²(x/2) e otteniamo
sen x = 2tg(x/2)/(1+tg²(x/2))

Identica dimostrazione per cos x
cos x = cos(2*x/2) = (cos²(x/2)-sen²(x/2))/1 = (cos²(x/2)-sen²(x/2))/(sen²(x/2)+cos²(x/2))
ora dividiamo tutto per cos²(x/2) e otteniamo
cos x = (1-tg²(x/2))/(1+tg²(x/2))

Per tg x si ha...
tg x = sen x / cos x = 2tg(x/2)/(1-tg²(x/2))

...e per ctg x vediamo...
ctg x = 1 / tg x = (1-tg²(x/2))/2tg(x/2)

N.B. Quando si utilizzano queste formule si deve cosidirerare l'esistena di tg(x/2) quindi si deve imporre: cos(x/2)!=0 ==> (x/2)!=(k+1/2)pi ==> x != (2k+1)pi

Identità goniometriche

Si definisce identità goniometrica ogni eguaglianza tra espressioni, che contengono fuzioni goniometriche di uno o più angoli, che è verificata qualunque siano i valori che si attribuiscono alle misure degli angoli contenuti (esclusi quei valori per i quali almeno una delle due espressioni perde significato)

Ad esempio un'identità potrebbe essere la seguente:
(sen 2x)(tg x) = 2sen²x
La dimostrazione è anche abbastanza banale:
(sen 2x)(tg x) = 2(sen x)(cos x)(sen x/cos x) = 2sen²x
Molte volte però si chiede di verificare identità di una complessità maggiore come la seguente:
sen(2x)/(1+cos(2x)) = tg x
(sen a-sen b)/(cos x+cos y) = tg((x-y)/2)
Ed ecco le dimostrazioni:
sen(2x)/(1+cos(2x)) = 2(sen x)(cos x)/(2-2sen²x) = (sen x)(cos x)/(1-sen²x) = (sen x)(cos x)/(cos²x) = sen x/cos x = tg x

(sen x-sen y)/(cos x+cos y) = 2(sen((x+y)/2))(cos((x-y)/2)) / 2(cos((x+y)/2))(cos((x-y)/2)) = sen((x+y)/2)/cos((x+y)/2) = tg((x+y)/2)

Equazioni goniometriche elementari

Un'equazione lineare si dice semplice quando è un'equazione del tipo
sen x=a oppure cos x=b , tg x=c , ctg x=d
la risoluzione di un'equazione lineare semplice consiste nel trovare gli angoli che sostituiti nell'equazione la verificano. Ad es.:

Equazioni goniometriche

Questo tipo di equazione pone una relazione tra due angoli o funzioni. Ad es.:
sen(3x+pi) = cos(4x-pi/2)
La risoluzione di questa equazione prevede l'utilizzo di questa tabella riassuntiva.

Dunque tornando alla nostra equazione sen(3x+pi) = cos(4x-pi/2), vediamo che le soluzioni sono:
(3x+pi)+(4x-pi/2) = (2k+1/2)pi
(3x+pi)-(4x-pi/2) = (2k+1/2)pi
risolvendo la prima si ha:
7x+pi/2 = pi/2+2k pi ==> 7x = 2k pi ==> x = 2k pi/7
e l'altra soluzione:
-x+3pi/2 = pi/2+2k pi ==> -x = -pi+2k pi ==> x = pi+2k pi ==> x = (2k+1)pi
Probabilmente avrai notato che quando ho cambiato entrambi i termini di segno, non ho cambiato di segno 2k pi e ciò perché k è un numero intero relativo (...,-3,-2,-1,0,1,2,3,ecc..) e quindi non cambierebbe assolutamente nulla nel cambiare di segno il periodo.

Equazioni lineari in sen x e cos x

Le equazioni lineari in sen x e cos x sono del tipo:
a sen x + b cos x = c
Ci sono 3 metodi per risolvere un'equazione lineare in sen x e cos x:
prendiamo come equazione-test sen x + sqr(3)cos x = 1

Primo metodo con le formule parametriche

Utilizzando le formule parametriche si rende l'equazione così:
t=tg(x/2)
2t/(1+t²) + sqr(3)(1-t²)/(1+t²) = (1+t²)/(1+t²)
eliminando il denominatore in quanto è uguale per tutti e tre gli addendi ed è sempre diverso da zero...
2t + sqr(3) - sqr(3)t² = 1 + t²
(1+sqr(3))t² - 2t + (1-sqr(3)) = 0
risolvendo l'equazione di secondo grado si ottiene
t = 1 e t = -2+sqr(3)
tg(x/2) = 1 ==> x/2 = pi/4+k pi ==> x = pi/2+2k pi
tg(x/2) = -2+sqr(3) ==> x/2 = -pi/12+k pi ==> x = -pi/6+2k pi
N.B. Con le formule parametriche si perde la potenziale soluzione x=(2k+1)pi per il motivo spiegato nella lezione precedente. Infatti se alla fine della risoluzione si accede ad una equazione di primo grado e non di secondo, la seconda soluzione è rappresentata proprio da (2k+1)pi. Comunque per andare sul sicuro è buona norma (o almeno lo consiglio io!) sostituire ad x il valore (2k+1)pi e vedere se si verifica l'equazione. In questo caso comunque avremmo -sqr(3)=1 in caso di sostituzione quindi siamo certi di non aver perso alcuna soluzione.

Secondo metodo con la circonferenza associata

Sia    Y=sen x e X=cos x   l'equazione diventa così:
Y + sqr(3)X = 1
si mette a sistema questa equazione con
X²+Y² = 1
quest'ultima non è altro che la'equazione della circonferenza goniometrica. Mettere a sistema significa trovare l'intersezione tra questa circonferenza e la retta Y + sqr(3)X = 1. Si risolve quindi il sistema...
Y = 1-sqr(3)X ==> sostituendo nell'equazione della circonferenza goniometrica ==>
X²+(1-sqr(3)X)² = 1 ==> X²+1+3X²-2sqr(3)X = 1 ==> 4X²-2sqr(3)X=0
ci sono due soluzioni per X:
X = 0 ==> Y = 1-sqr(3)*0 = 1
X = sqr(3)/2 ==> Y = 1-sqr(3)*sqr(3)/2 = -0.5

Terzo metodo

Questo è un metodo un pò meno rigoroso e che, soprattutto, solo raramente può essere applicabile. La sua relativa semplicità però ci induce a trattarlo.
sen x + sqr(3)cos x = 1
divido tutto per 2
1/2*sen x + sqr(3)/2*cos x = 1/2
1/2 non è altro che il coseno di pi/3 e sqr(3)/2 è il seno di pi/3, dunque:
cos(pi/3)sen x + sen(pi/3)cos x = 1/2
ma il primo termine dell'uguaglianza non è altro che...
sen(pi/3 + x) = 1/2
Due angoli hanno per seno 1/2: pi/6 e 5pi/6
pi/3 + x = pi/6+2k pi ==> x = -pi/6 +2k pi
pi/3 + x = 5pi/6+2k pi ==> x = pi/2 +2k pi
N.B. Quando invece (sen x) e (cos x) hanno lo stesso coefficiente (occhio al segno!) è possibile dividere tutto affinché entrambi abbiano per coefficiente 1/sqr(2). Ad es.:
14sen x + 14cos x = 6
divido tutto per 14*sqr(2)
(sen x)/sqr(2) + (cos x)/sqr(2) = 6/(14sqr(2))
(sen x)(cos pi/4) + (cos x)(sen pi/4) = 3/(7sqr(2))
sen(x+pi/4) = 3/(7sqr(2)) ecc....

Equazioni omogenee in sen x e cos x

Le equazioni omogenee presentano tutti gli addendi di uno stesso grado:
sen²x + 4(sen x)(cos x) + 3cos²x = 0
per risolvere questo tipo di equazioni di n° grado basta dividere tutto per cosⁿx
tg²x + 4tg x + 3 = 0
le soluzioni di questa equaziono sono:
tg x = -1 ==> x = -pi/4 + k pi
tg x = -3 ==> x = -pi/3 + k pi
Attenzione !!! Prima di dividere tutto per cosⁿx bisogna fattorizzare cos x ovunque sia possibile farlo. Mi spiego meglio: se abbiamo
2(sen x)(cos x) + 5cos²x = 0
in questo caso è possibile fattorizzare cos x e quindi l'equazione diventa:
(cos x)(2sen x + 5cos x) = 0
così per trovare le soluzioni eguagliamo a zero il primo e il secondo fattore.

Le equazioni omogenee in sen x e cos x possono tranquillamente essere risolte se sono anche di grado superiore al secondo:
sen⁴x - 4(sen²x)(cos²x) + 3cos⁴x = 0
Dopo aver constatato l'impossibilità di fattorizzare cos x si divide tutto per cos⁴x
tg⁴x - 4tg²x + 3 = 0
(tg²x-3)(tg²x-1) = 0
Ci sono 4 soluzioni:

• tg x = sqr(3) ==> x = pi/3 +k pi
• tg x = -sqr(3) ==> x = -pi/3 +k pi
• tg x = 1 ==> x = pi/2 +k pi
• tg x = -1 ==> x = -pi/2 +k pi

Risolviamo ora un'equazione di 8° grado:
(sen⁶x)(cos²x) - 4(sen⁴x)(cos⁴x) + 3(sen²x)(cos⁶x) = 0
Sembra difficile...ma non lo è! Prima di tutto dobbiamo fattorizzare cos²x
(cos²x)*((sen⁶x) - 4(sen⁴x)(cos²x) + 3(sen²x)(cos⁴x)) = 0
ora dividiamo il secondo trinomio per cos⁴x
(cos²x)*(tg⁶x - 4tg⁴x + 3tg²x) = 0
scomponiamo con Ruffini il trinomio e alla fine otteniamo
(cos²x)*(tg²x)(tg²x - 1)(tg²x - 3) = 0
le soluzioni sono moltiplici:

• cos x = 0 ==> x = (k+1/2)pi
• tg x = 0 ==> x = k pi
• tg x = +1 ==> x = pi/4 +k pi
• tg x = -1 ==> x = -pi/4 +k pi
• tg x = sqr(3) ==> x = pi/3 +k pi
• tg x = -sqr(3) ==> x = -pi/3 +k pi

Sistema per rendere omogenee le equazioni e le disequazioni goniometriche

Purtroppo non capita molto spesso di avere a che fare con disequazioni omogenee in sen x e cos x. Ad esempio.:
6sen²x + 3cos²x - 5 = 0
Questa chiaramente non è un'equazione omogenea tuttavia c'è un sistema per farla diventare tale: in questo caso basta moltiplicare il termine noto -5 per sen²x+cos²x, quantità che per la prima relazione fondamentale della trigonometria è uguale a 1, ed ecco il risultato:
6sen²x + 3cos²x - 5sen²x - 5cos²x = 0 ==> sen²x - 3cos²x = 0
questo sistema è applicabile anche ad equazioni di grado più alto: noi possiamo moltiplicare tutto quello che ci pare per sen²x+cos²x senza problemi. Dunque facendo un altro esempio:
7sen⁴x + 5cos⁴x - 3 = 0
in questo caso devo portare tutto al 4° grado quindi devo moltiplicare il termine noto per (sen²x+cos²x)²
7sen⁴x + 5cos⁴x - 3sen⁴x - 3cos⁴x - 6(sen²x)(cos²x) = 0 ==>
==> 4sen⁴x - 6(sen²x)(cos²x) + 2cos⁴x = 0
Facile vero? Questo sistema vi potrebbe tornare utile molto spesso.
N.B. Questo sistema può essere tranquillamente utilizzato anche nelle disequazioni goniometriche.

Disequazioni goniometriche elementari

Si definisce disequazione goniometrica una disequazione in sinx e/o cosx

esempio:
sinx > 1/2
Per risolvere la precedente disequazione si possono utilizzare due differenti algoritmi:

1. Metodo della circonferenza goniometrica
   Si disegna la circonferenza goniometrica e si intercettano su di essa gli angoli per i quali la disequazione è nulla;
   basterà poi segnare, a partire da quegli angoli, l'arco per il quale è verificata la disequazione, cioè sinx è maggiore di 1/2
   
   
2. La disequazione goniometrica è trattata come una normale disequazione
   (metodo ottimo nel caso di disequazioni goniometriche fratte)

Disequazioni goniometriche omogenee in sen x e cos x

1. Il grado di omogeneità sia pari
   
   sqr(3)sin²x - 2sinxcosx - sqr(3)cos² < 0
   
   Si divide la dsequazione per cosⁿx che, essendo n pari, è un numero positivo,
   sqr(3)tg²x - 2tgx - sqr(3) < 0
   
   tgx = sqr(3)
   tgx = -1/sqr(3)
   
      SOLUZIONI:

2. Il grado di omogeneità è dispari
   
   sinx + cosx > 0
   
   Si divide per cosⁿx, con n grado di omogeneità dispari:
   cosⁿx è positivo se cosx è positivo;
   cosⁿx è negativo se cosx è negativo:
   pertanto, quando dividiamo la disequazione data per cosⁿx, dobbiamo tener conto della possibile negatività del denominatore, e per questo la disequazione data sfocia in due disequazioni in tgx:
• una dello stesso segno della disequazione data, a sistema con cosx > 0 ;
• l'altra di segno opposto rispetto alla disequazione data, a sistema con cosx < 0 .

Il primo sistema sarà costituito dalle disequazioni:
tgx + 1 > 0
cosx > 0

   SOLUZIONI:

Il secondo sistema sarà costituito dalle disequazioni:
tgx + 1 < 0
cosx < 0
   SOLUZIONI:

SOLUZIONI DEL SISTEMA:

Disequazioni goniometriche lineari in sen x e cos x

1. Con uso delle formule parametriche
   
   sinx + cosx - 1 < 0
   
   Usando le formule parametriche:
   [2 tgx/2 + (1 - tg²x/2) - (1 + tg²x/2)] / (1 + tg²x/2) < 0
   Il binomio (1 + tg²x/2) può essere eliminato poiché positivo e diverso da zero, quindi
   [2 tgx/2 + (1 - tg²x/2) - (1 + tg²x/2)] / (1 + tg²x/2) < 0
   
   - tg²x/2 + tgx/2 < 0
   
      SOLUZIONI:

2. Con uso della circonferenza goniometrica associata e orientamento di una retta

3. 
   Utilizzando il metodo precedentemente descritto possiamo risolvere anche le disequazioni goniometriche lineari:
   
   
   esempio:
   
   Risolvere l'equazione sinx + cosx - 1 >0
   Sia sinx = Y
   cosx = X
   Di conseguenza la disequazione diventerà:
   X + Y - 1 > 0 che risolta con il suddetto metodo, e messa a sistema con la circonferenza goniometrica (X² + Y² = 1), ci fornirà l'intervallo desiderato.
   
      SOLUZIONI:

5. Metodo rapido
   
   In alcuni casi è possibile utilizzare degli espedienti per semplificare il calcolo.
   Nel nostro caso ad esempio dividendo l'equazione per sqr(2), otteniamo l'equazione:
   
   (sinx)/sqr(2) + (cosx)/sqr(2) > 1/sqr(2)
   Ma questa equazione è riconducibile, considerando quell' 1/sqr(2) come sin45° e cos45°, all'equazione:
   sin (x + 45°) > 1/sqr(2)
   
   Chiamando (x + 45°) = y :
   
      SOLUZIONI:

6. 
   
   E quindi risostituendo:
   
      SOLUZIONI:

1° Teorema sui triangoli rettangoli

In un triangolo rettangolo la misura di un cateto è uguale al prodotto della misura dell'ipotenusa per il seno dell'angolo ad esso opposto, o per il coseno dell'angolo ad esso adiacente

2° Teorema sui triangoli rettangoli

In un triangolo rettangolo la misura di un cateto è uguale alla misura dell'altro cateto per la tangente dell'angolo ad esso opposto, o per la cotangente dell'angolo ad esso adiacente.

Teorema della corda

La lunghezza di una corda in una C(circonferenza) di raggio r è uguale al diametro della circonferenza per il seno dell'angolo alla circonferenza che insiste su uno dei due archi sottesi alla corda.

Teorema dei seni (o di Eulero)

In un triangolo qualsiasi la misura dei lati è proporzionale al seno degli angoli opposti.

Teorema delle proiezioni

In un triangolo qualsiasi la misura di un lato è uguale alla somma algebrica delle proiezioni degli altri due lati su di esso, quindi alla somma dei prodotti delle misure di ciascuno degli altri due lati per il coseno dell'angolo che ognuno di essi forma con il lato considerato.

Teorema del coseno (o di Carnot)

In un triangolo qualsiasi la misura al quadrato di un suo lato è uguale alla somma dei quadrati degli altri due diminuiti del doppio prodotto di essi per il coseno dell'angolo che questi ultimi due formano tra loro.

Formule di Briggs

Area di un triangolo noti i due lati e l'angolo tra essi compreso

L'area di un triangolo è uguale al semiprodotto dei lati per l'angolo tra essi compreso.

Area di un triangolo noti i lati (formula di Erone)

L'area di un triangolo è uguale alla radice quadrata del prodotto tra semiperimetro per semiperimetro meno a, per semiperimetro meno b, per semiperimetro meno c.

Misura del raggio della circonferenza inscritta in un triangolo noti 3 lati

Misura del raggio della circonferenza circoscritta in un triangolo noto un lato e l'angolo opposto

Misura del raggio della circonferenza circoscritta in un triangolo noti 3 lati

Misura di una mediana noti i 3 lati

Misura di una bisettrice noto angolo diviso e lati adiacenti

Area di un quadrilatero qualunque note le diagonali e un angolo che esse formano