|
|
| |
PUNTI DI DISCONTINUITA' ED ESEMPI GRAFICI
Un punto x0 di un intervallo [a;b] si dice punto di discontinuità per una funzione f(x) se la funzione è definita in tutto l'intervallo [a;b], escluso al più x0, e in tale punto essa non è continua. I punti di discontinuità possono essere di tre specie:
I SPECIE lim f(x)= lim f(x)=
x → x0+ x → x0-
Un punto di discontinuità è di prima specie se calcolando il limite per x che tende ad x0 da destra e da sinistra si ottengono due valori finiti differenti.
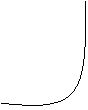
II SPECIE lim f(x)=∞
x → x0
Un punto di discontinuità è di seconda specie se calcolando il limite per x che tende ad x0 si ottiene come risultato infinito.
III SPECIE lim f(x)=
x → x0
Un punto di discontinuità è di terza specie se calcolando il limite per x che tende ad x0 si da destra che da sinistra si ottiene lo stesso valore finito.
Es.:
![]()

![]() y x0
y x0
![]() 0 x
0 x
CONCETTO DI CONTINUITA' ED ESEMPIO GRAFICO
La funzione f(x)si dice continua nel punto x0 quando il lim f(x)=f(x0) .
x → x0
Affinché la funzione sia continua occorre che siano rispettate tre condizioni:
f(x0)
lim f(x)=
x → x0
= f(x0)
Deve cioè esistere il limite di f(x) per x che tende ad x0 e tale limite deve essere uguale a f(x0). Se una di queste tre condizioni dovesse cadere, la funzione non sarebbe continua.
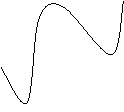
Es.: funzione continua
In [a;b]
![]()
![]()
![]() y
y
![]()
0 a b x
Non è detto che una funzione continua sia derivabile, mentre ogni funzione derivabile in un punto è ivi continua.
ASINTOTI
Gli asintoti sono delle linee rette alle quali la curva della funzione si avvicina senza mai toccarle. Gli asintoti possono essere verticali, orizzontali od obliqui.
ASINTOTI VERTICALI: x = x0
lim f(x)=∞
x → x0
Gli asintoti verticali si trovano calcolando il limite per x che tende al valore escluso dal dominio, ovvero dall'insieme di tutti i valori che si possono attribuire ad x, della funzione. Affinché ci sia l'asintoto verticale deve risultare infinito.
ASINTOTI ORIZZONTALI: y =
lim f(x)=
x → ∞
Gli asintoti orizzontali si trovano calcolando il limite per x che tende ad infinito della funzione. Affinché ci sia l'asintoto orizzontale deve risultare un numero finito.
ASINTOTI OBLIQUI: y=mx+q
Bisogna calcolare m.
lim f(x) =
x → ∞ ‾‾‾‾x‾‾‾‾
... e q
lim f(x) - mx
x → ∞
Per ricavare gli asintoti obliqui bisogna prima trovare il coefficiente angolare (m) della retta, calcolando il limite per x che tende ad infinito della funzione alla quale si aumenta di un grado l'incognita del denominatore. Deve risultare un numero finito altrimenti l'asintoto è orizzontale. Poi si passa a trovare il punto di intersezione della retta con l'asse delle ordinate (q), calcolando, della differenza fra la funzione e la funzione calcolata in m, il limite per x che tende ad infinito. Se l'asintoto attraversa l'asse delle y, deve risultare un numero finito.
SIGNIFICATO GEOMETRICO DELLA DERIVATA PRIMA
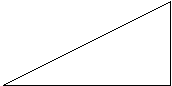
La derivata prima di una funzione f(x) è il limite per h che tende a 0 del rapporto incrementale della funzione nel punto c del suo dominio.
f(c+h) - f(c)
h
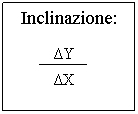
![]() Il rapporto incrementale R= dà l'inclinazione della
retta che congiunge A e B, secondo il 2° teorema fondamentale della
trigonometria, secondo il quale b/c=tgβ.
Il rapporto incrementale R= dà l'inclinazione della
retta che congiunge A e B, secondo il 2° teorema fondamentale della
trigonometria, secondo il quale b/c=tgβ.
Geometricamente la derivata prima dà il coefficiente angolare della tangente in A.

![]()
ΔY ΔX
|
|
|
|
|
|
|
|
|
|
DEFINIZIONE DI FUNZIONE CRESCENTE IN (a;b) E METODO DI RICONOSCIMENTO
Una funzione è crescente in un intervallo se
x1, x2 Df; x1 < x2 → f(x1) < f(x2)
Dati due x, valori non esclusi dal dominio della funzione, e se all'aumentare di questi corrisponde l'aumentare delle y, la funzione è crescente.
Es. grafico di funzione crescente:
![]()

![]()
![]() f(x2)
f(x2)
![]()
![]() f(x1)
f(x1)
x1 x2
![]()
Per riconoscere se una funzione è crescente bisogna studiare il segno della sua derivata prima. Negli intervalli positivi è crescente, mentre in quelli negativi è decrescente. Studiando il segno della derivata prima si individuano anche i punti stazionari.
La derivata prima di una funzione serve, inoltre, ad individuare l'equazione della tangente in un punto.
APPLICAZIONI DELLA DERIVATA SECONDA
La derivata seconda si ottiene derivando due volte la funzione, ovvero riderivando la derivata prima.
La derivata seconda di una funzione serve per individuare:
CONCAVITA' O CONVESSITA' DELLA CURVA DELLA FUNZIONE
Se f"(x)>0 allora la concavità sarà rivolta verso l'alto;
Se f"(x)<0 allora la concavità sarà rivolta verso il basso.
PUNTI DI FLESSO A TANGENTE OBLIQUA:
Perché ci siano flessi a tangente obliqua f"(x)=0, cioè la derivata seconda deve essere uguale a 0. Si procede poi trovando l'equazione della retta tangente a quel punto, sostituendo a y - y0 = f'(x) (x - x0) , equazione del fascio di rette passanti per un punto, i valori necessari. f'(x), ovvero la derivata prima, dà il coefficiente angolare della retta.
PUNTI STAZIONARI:
La derivata seconda permette di evitare lo studio del segno della derivata prima per individuare i punti stazionari.
Se f"(x0)>0, il punto è un minimo;
Se f"(x0)<0, il punto è un massimo;
Se f"(x0)=0, non si può determinare e si va alle derivate successive fino a che non risultino diverse da 0. In tale caso il punto sarà un flesso a tangente orizzontale.
DEFINIZIONE DI PUNTO STAZIONARIO E METODO DI RICERCA
I punti stazionari sono gli zeri della derivata prima, ovvero le soluzioni dell'equazione. Quindi, affinché ci siano punti stazionari f'(x)=0.
Se la tangente della funzione nel punto è parallela all'asse delle ascisse i punto P(x0; y0) è stazionario.
I punti stazionari possono essere
DI MASSIMO:
x a; b f(x) ≤ f(x0)
Se per ogni x appartenente ad un certo intervallo f(x) è minore o tutt'al più uguale a f(x0)
DI MINIMO:
x a; b f(x) ≥ f(x0)
Se per ogni x appartenente ad un certo intervallo f(x) è maggiore o tutt'al più uguale a f(x0)
DI FLESSO:
Data la funzione y = f(x) definita e continua in un certo intervallo, si dice che presenta in x0, interno all'intervallo, un punto di flesso se in tale punto il grafico di f(x) cambia concavità. In un punto in cui esiste la tangente, un flesso può essere:
- orizzontale se la tg nel punto è parallela all'asse delle x;
- obliquo se la tg non è parallela ad uno degli assi.
I punti di massimo, di minimo, e di flesso a tg orizzontale si trovano studiando il segno della derivata prima. I punti in cui la curva da crescente inizia a decrescere sono di massimo, viceversa di minimo, e se continua a crescere o decrescere ma cambiando concavità sono di flesso.
I punti stazionari, compreso il flesso a tg obliqua, si possono anche individuare con la derivata seconda che permette di evitare lo studio del segno della derivata prima per individuare i punti stazionari.
Se f"(x0)>0, il punto è un minimo;
Se f"(x0)<0, il punto è un massimo;
Se f"(x0)=0, non si può determinare e si va alle derivate successive fino a che non risultino diverse da 0. In tale caso il punto sarà un flesso a tangente orizzontale.
Perché ci siano flessi a tangente obliqua f"(x)=0, cioè la derivata seconda deve essere uguale a 0. Si procede poi trovando l'equazione della retta tangente a quel punto, sostituendo a y - y0 = f'(x) (x - x0) , equazione del fascio di rette passanti per un punto, i valori necessari. f'(x), ovvero la derivata prima, dà il coefficiente angolare della retta.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024