|
|
| |
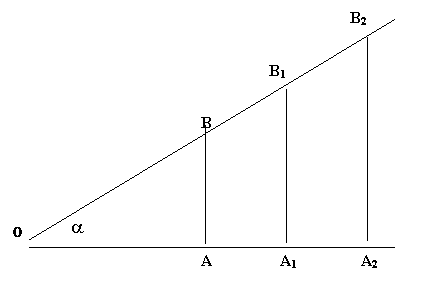
Attraverso lo studio di triangoli simili AOB ,A1OB1 ,A2OB2 :
Possiamo constatare che questi triangoli sono simili in quanto hanno un angolo a e due lati ordinatamente in proporzione e con ciò siamo in grado attraverso la trigonometria di calcolare il valore delle diverse funzioni trigonometric 414c28e he;
Le funzioni trigonometric 414c28e he più importanti sono il seno di a,il coseno di a e la tangente di a
Il seno di a è il rapporto fatto tra il cateto opposto all'angolo e l'ipotenusa:
BA B1A1 B2A2
![]()
![]()
![]() Seno di a
Seno di a
OB OB1 OB2
Il grafico della funzione seno di a è il seguente: 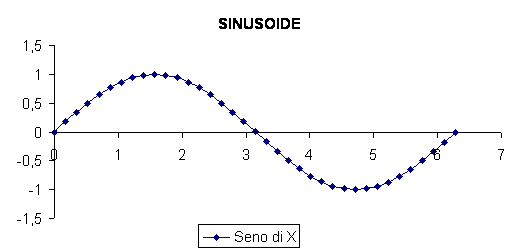
Attraverso questo grafico siamo in grado di dimostrare che la funzione seno di a è simmetrica rispetto all'origine, possiamo constatare anche che tale funzione è crescente con valori compresi (prendendo in considerazione un angolo giro) tra 270° e 90° il valore della funzione va da -1 a +1;la funzione è invece decrescente con angoli compresi tra 90° e 270°, il valore della funzione va in questo caso da +1 a -1.
Il coseno di a corrisponde al rapporto fatto tra il cateto adiacente all'angolo e l'ipotenusa:
OA OA1 OA2
![]()
![]()
![]() Coseno di a
Coseno di a
OB OB1 OB2
Il grafico della funzione coseno di a è il seguente:
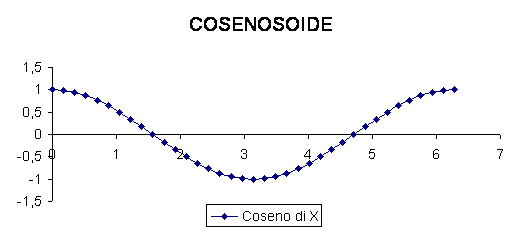
Attraverso questo grafico siamo in grado di dimostrare che la funzione coseno di a è simmetrica rispetto all'asse delle ordinate, possiamo constatare anche che tale funzione è crescente con valori compresi (prendendo in considerazione un angolo giro) tra 180° e 360° il valore della funzione in questo caso va da -1 a +1;la funzione è invece decrescente con angoli compresi tra 0° e 180°, il valore della funzione va in questo caso da +1 a -1.
La tangente di a è uguale al rapporto fatto il cateto opposto all'angolo e il cateto adiacente all'angolo:
BA B1A1 B2A2 seno di a
![]()
![]()
![]()
![]() Tangente dia
Tangente dia
OA OA1 OA2 coseno di a
Il grafico della funzione tangente di a è il seguente: 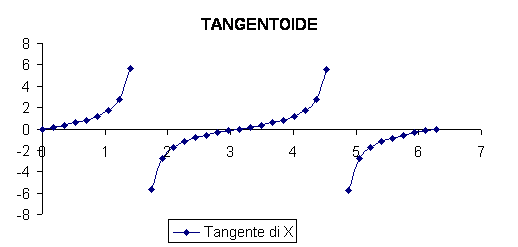
Attraverso questo grafico siamo in grado di dimostrare che la funzione tangente di a è periodica di periodo 180°, possiamo constatare anche che tale funzione è crescente con valori compresi (prendendo in considerazione un angolo giro) tra 271° e 89° e anche con valori compresi tra 91° e 269° ;in questa funzione ci sono dei valori di discontinuità che sono anch'essi periodici di 180° che sono: + 90° e -90°, + 270° e -270° ecc. ecc..
La cosecante di a corrisponde al rapporto inverso del seno di a ;ossia basta fare un rapporto tra ipotenusa e cateto opposto all'angolo.
OB OB1 OB2 1
![]()
![]()
![]()
![]() Cosecante di a
Cosecante di a
BA B1A1 B2A2 seno di a
Il grafico della funzione cosecante di a è il seguente:
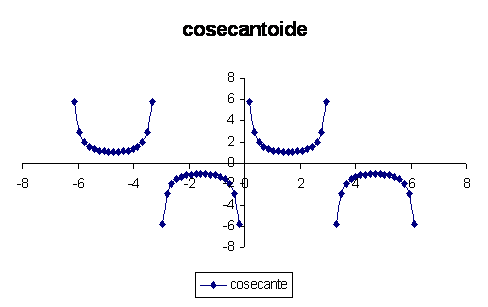
Attraverso questo grafico siamo in grado di dimostrare che la funzione cosecante di a può avere delle relazioni con la funzione tangente per quanto riguarda i punti di discontinuità, tali punti corrispondono agli angoli: 0°, +180° e -180° ,+360° e -360°, possiamo quindi capire che c'è periodicità della funzione di 180°; possiamo constatare anche che tale funzione è crescente con valori compresi (prendendo in considerazione la parte di grafico di destra) tra 90° e 279° e anche con valori compresi tra 181° e 270°; la funzione è decrescente con valori compresi tra 1° e 90° e anche con valori compresi tra 270° e 359°; prendendo ora in considerazione la parte di sinistra possiamo constatare che tale funzione è crescente con valori compresi invece tra -270° e -181° e anche con valori compresi tra -179° a -90°; la funzione è decrescente con valori compresi tra -359° a -270° e anche con valori compresi tra -90° e-1°.
La secante di a
La secante di a corrisponde al rapporto inverso del coseno di a ;ossia basta fare un rapporto tra ipotenusa e cateto adiacente all'angolo.
OA OA1 OA2 1
![]()
![]()
![]()
![]() Secante di a
Secante di a
OB OB1 OB2 Coseno di a
Il grafico della funzione secante di a è il seguente:
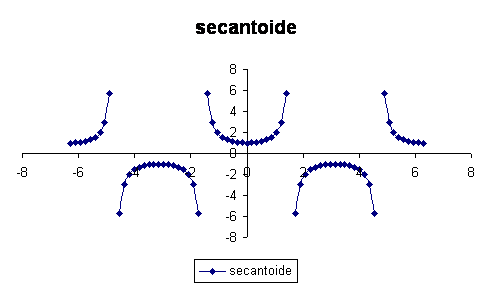
Attraverso questo grafico siamo in grado di dimostrare che la funzione secante di a è simmetrica rispetto all'asse delle ordinate; può avere anche delle relazioni con la funzione tangente e cosecante di a per quanto riguarda i punti di discontinuità, tali punti corrispondono agli angoli: +90 e -90, +270° e -270° ecc. ecc. , possiamo quindi capire che c'è periodicità della funzione di 180°; un'altra cosa è che tale funzione è crescente con valori compresi (prendendo in considerazione la parte di grafico di destra)tra 0° e 89° e anche con valori compresi tra 91° e 180°; la funzione è decrescente con valori compresi tra 180° e 269° e anche con valori compresi tra 271° e 360°; prendendo ora in considerazione la parte di sinistra possiamo constatare che tale funzione è crescente con valori compresi invece tra -360° e -271° e anche con valori compresi tra -269° e -91°; la funzione è decrescente con valori compresi da -180° a -91° e anche con valori compresi tra -89° e 0°.
La cotangente di a corrisponde al rapporto inverso della tangente di a;ossia basta fare in questo caso un rapporto tra cateto adiacente all'angolo e cateto opposto all'angolo; possiamo anche dire che equivale al rapporto tra coseno di a e il seno di a
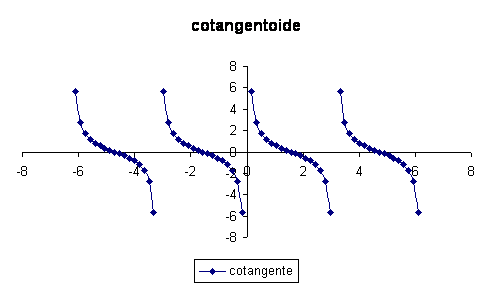
Il grafico della cotangente di aè il seguente:
Attraverso questo grafico siamo in grado di dimostrare che la funzione cotangente di a può avere delle relazioni con la funzione tangente di a per quanto riguarda i punti di discontinuità, tali punti corrispondono agli angoli: 0, +180 e -180 , +360° e -360° ecc. ecc. , possiamo quindi capire che c'è periodicità della funzione di 180°; un'altra cosa è che tale funzione è solamente decrescente (come si può constatare dal grafico) ossia le linee che formano le parabole vanno dal quadrante delle ordinate positive al quadrante delle ordinate negative; la funzione è quindi "studiabile" con valori che vanno da -359° a -181°, tra -179° e -1° , tra +1° e +179° e tra +181° e +359°.
Possiamo constatare anche che il grafico corrisponde al grafico della funzione tangente solamente girato di 180°.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024