LA VARIABILITA'

In particolare la variabilità misura la diversità fra le modalità di un fenomeno. Si possono considerare  tre tipi distanze:

fra ogni termine della distribuzione e la media;

fra i termini della distribuzione;

fra particolari termini della distribuzione.

Per valutare la distanza fra ogni elemento della distribuzione e la media useremo gli scostamenti medi; per le distanze fra i vari elementi della distribuzione calcoleremo le differenze medie ed infine per le distanze fra particolari elementi della distribuzione utilizzeremo gli intervalli di variazione. Per tutte le applicazioni che di seguito vedremo consideriamo la seguente distribuzione di frequenze:

Tabella  1

 

    Scostamenti  medi

Come già detto, con gli scostamenti vado a studiare la distanza fra ogni elemento della distribuzione e una qualsiasi media, che in questo contesto indicheremo con M.

  In particolare lo scostamento medio di ordine r da M per la distribuzione di frequenze vista è calcolabile attraverso la seguente relazione:

 

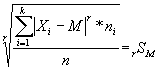
   Importante proprietà di tale scostamento è la seguente:   rS_M >= 0

       Dando all'indice r particolari valori, si ottengono particolari tipi di scostamenti:

   Scostamenti semplici medi     

       Questo tipo di scostamento si ottiene, semplicemente ponendo nella formula generale rS_M  il valore r = 1 . Come al solito, nella formula indicheremo con M una generica media, o meglio, un generico centro; in particolare calcolando lo scostamento dalla mediana Me si ottiene il più piccolo degli scostamenti semplici medi.

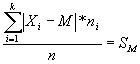
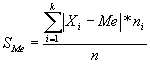
   Nel caso in cui il carattere sia diviso in classi, per calcolare tutti gli scostamenti si dovrà far riferimento al valore centrale della classe (assumendo, come si è fatto per il calcolo delle medie, che tutte le unità all'interno della classe presentino modalità pari al valore centrale della classe); per rinfrescare la memoria in merito consulta " Le medie" a pag.3.

   Scostamenti quadratici medi

   Analogamente a quanto visto per gli scostamenti semplici, gli scostamenti quadratici medi, si ottengono ponendo r = 2 :

  

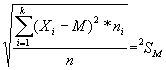
    Il più importante scostamento all'interno di questo gruppo è quello che si calcola dalla media aritmetica, in particolare esso è il più piccolo scostamento quadratico e prende anche il nome di σ (sigma).  Elevando tale quantità al quadrato si ottiene un importante indicatore della variabilità: la varianza.

Differenze  medie  

In alcuni studi capita che la scelta della media da cui calcolare gli scostamenti non sia importante; in questi casi si può ricorrere al calcolo della disuguaglianza dei termini fra loro. Per capire meglio la situazione consideriamo una distribuzione unitaria:

a₁, a₂, ...,a_n

Tentiamo di scrivere tutte le differenze calcolabili:

Tabella  2

 

Anche per le differenze medie esiste una formula generale, relativa ad un indice r, variabile al variare di r stesso. 

Nel calcolo della differenza media di ordine r possiamo considerare le differenze di ogni elemento da se stesso (ovviamente nulle) poste sulla diagonale principale della tabella 2, dando vita alla differenza media con ripetizione di ordine r. Analogamente posso escludere dal calcolo le differenze sulla diagonale ottenendo la differenza media senza ripetizione di ordine r;

   

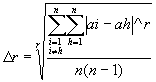
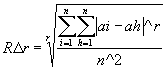
Numericamente il numeratore assume lo stesso valore in entrambe le formule, il denominatore è ovviamente diverso, infatti nella prima formula ( senza ripetizione ) troviamo n(n-1) che è esattamente il numero di differenze che prendiamo in considerazione; nella seconda formula abbiamo  n^2, cioè tutte le differenze comprese quelle sulla diagonale.

Intervalli  di  variazione

Il più importante intervallo di variazione è il campo di variazione, corrispondente al termine inglese range, ottenuto dalla differenza fra il valore massimo della distribuzione e quello minimo:

W =X_(n) - X₍₁₎

 dove  X_(n) è il valore massimo e  X₍₁₎ è il valore minimo..

Altro intervallo è la cosiddetta differenza interquartile     Q = Q₃ - Q₁ ;  dividendo tale quantità per 2 troviamo la semidifferenza interquartile.

Indici di variabilità

Gli  indici assoluti di variabilità sono espressi nella stessa unità di misura della distribuzione; è ovvio che in questa condizione è difficile fare confronti fra distribuzioni diverse. Per  risolvere questo ed altri problemi è utile dividere ogni indice assoluto di variabilità per una media; da evidenziare in tale ambito è il coefficiente di variazione  CV dato dalla seguente relazione 

Lo scopo della lezione appena terminata è quello di prendere confidenza con il concetto di variabilità ed i più usati indici come la varianza e lo scarto quadratico medio.

LE MEDIE

Domande

• Qual è lo scopo dello studio della variabilità di un fenomeno?
• Qual è il significato statistico della varianza?
• Perchè è importante il calcolo della varianza?
• Che differenza c'è fra differenze con e senza ripetizione?
• Che informazione ci fornisce il range?
  
  
  
  
  
  
  
  
  

Glossario

A

AREOGRAMMA

Particolare tipo di rappresentazione grafica in cui la frequenza o la quantità di una data modalità vengono rappresentate attraverso l'area di una figura piana. In particolare tale area dovrà essere proporzionale alla frequenza rappresentata.

AMPIEZZA DELLA CLASSE

L'ampiezza di una data classe si calcola facendo la differenza fra l'estremo superiore e quello inferiore della classe in esame.

C

CAMPIONE

Parte della popolazione costruita in modo tale da rappresentare al meglio la popolazione da cui viene estratto. Lo scopo della costruzione di un campione è quello di lavorare su un collettivo più piccolo della popolazione, per poi espandere i risultati ottenuti a tutta la popolazione.

CAMPO  DI  VARIAZIONE

Il campo di variazione è una misura della variabilità di una distribuzione e si ottiene calcolando la differenza fra il termine più grande e quello più piccolo della distribuzione.

CARATTERE

In ogni ricerca statistica studiamo una o più caratteristiche delle unità rilevate; queste caratteristiche vengono definite con il termine carattere. Il carattere si manifesta nelle unità attraverso varie modalità.

CENSIMENTO

Rilevazione generale della popolazione di un paese; il censimento si effettua ogni 10 anni e va a rilevare alcune caratteristiche di tutta la popolazione.

CENTRO

Data una distanza, il centro di una distribuzione è il valore che, rispetto alla distanza considerata, rappresenta al meglio la popolazione

CLASSI

Le classi sono il frutto della divisione delle modalità di un carattere in gruppi. In particolare,  le modalità di un carattere come il peso o l'altezza, per semplificare il lavoro, possono essere raggruppate insieme, creando un'unica modalità, generalmente rappresentata dal valore centrale della classe.

CONCENTRAZIONE

Attributo che si dà ad un carattere quantitativo trasferibile. Si dice che, in una distribuzione la concentrazione è massima quando tutto l'ammontare del carattere si trova in una sola unità; al contrario, si dice che un carattere è equidistribuito quando l'ammontare è equamente diviso fra tutte le unità della popolazione. La concentrazione rientra nelle misure della variabilità di una distribuzione.

COGRADUAZIONE

La tabella di cograduazione si calcola in ambito di dissomiglianza e serve per gestire più facilmente i dati cograduati. In particolare ci dice che modalità presentano i dati cograduati.

COGRADUATI (DATI)

Definiamo termini cograduati di una distribuzione quei termini che occupano lo stesso posto nella graduatoria dei termini di una distribuzione. 

D

DATO ANOMALO

Un dato è definito anomalo quando è molto diverso dagli altri dati della distribuzione. Tale diversità può attribuirsi ad errore (di rilevazione o inserimento) o all'inizio di una nuova fase del fenomeno.

DETERMINAZIONE (indice di)

Visto nell'ambito della regressione, l'indice r²  indica la bontà di accostamento di ciascuna delle rette di regressione ai dati osservati. Abbiamo che:

Se  r²  = 0 allora le due rette di regressione coincidono con gli assi cartesiani (con origine posta nel baricentro). Se  r² = 1 allora  i punti osservati sono allineati e le due rette di regressione sono sovrapposte. In altre parole, tanto più l'indice di determinazione è vicino a 1 tanto più le rette descriveranno meglio la distribuzione osservata.

DEVIANZA TOTALE

In ambito di regressione, definiamo devianza totale la distanza fra ogni valore osservato Y_j e la media  Y.  E' valida la seguente relazione:  DEV. TOT. = DEV. REG. + DEV. RES

DEVIANZA DI REGRESSIONE

In ambito di regressione è la distanza fra i valori teorici Y^*_j e la media Y. E' anche chiamata devianza spiegata dalla regressione.

DEVIANZA RESIDUA

In ambito di regressione, indica la distanza fra la distribuzione osservata e la distribuzione teorica rappresentata dai punti della retta di regressione. 

DIPENDENZA IN MEDIA

Data una distribuzione secondo due caratteri, diciamo che se Y è indipendente in media da X allora le distribuzioni parziali secondo il carattere Y hanno la stessa media aritmetica. Ricordiamo che una situazione di connessione nulla implica indipendenza in media. Un indice di dipendenza in media è quello proposto da Pearson  (vedi lezioni)  

che assume valore 1 nel caso di dipendenza perfetta di Y da X; assume invece valore 0 nel caso di indipendenza in media.

M

MODALITA'

Ogni carattere si presenta nelle unità attraverso delle modalità. Ad esempio il carattere sesso si presenta con le modalità maschio e femmina.

V

VALORE CENTRALE DI UNA CLASSE

Il valore centrale di una classe è la misura che più frequentemente si usa nelle elaborazioni di caratteri divisi in classi. Si trova sommando gli estremi della classe e dividendo il risultato per 2.