LA PROBABILITA' - NEL GIOCO DEL POKER - LA NASCITA DELLA TEORIA DELLA PROBABILITA'

LA NASCITA DELLA TEORIA DELLA PROBABILITA'

Il testo che segue è tratto da "febbre da gioco"

Il gioco dei dadi non ha solo introdotto dal punto di vista linguistico i termini "alea" e "azzardo", ma ha anche contribuito a far nascere una fondamentale teoria matematica: il calcolo delle probabilità.

Anche se alcuni studiosi ritengono che tale teoria si sia sviluppata essenzialmente grazie al contributo di studi meno futili, condotti in ambito economico e giuridico, è storicamente provato che i suoi primi concetti sono stati formulati affrontando problemi relativi al lancio dei dadi. Un tale accostamento, solo apparentemente irriverente, è giustificato dal fatto che le regole dei giochi d'azzardo si prestano a essere facilmente interpretate mediante un modello matematico pratico e funzionale, grazie alla loro sinteticità e linearità. Nel mondo antico, il concetto di probabilità era essenzialmente conosciuto in termini filosofici, rimanendone del tutto ignoti i risvolti matematici. Il motivo per cui questi ultimi furono trascurati risiede presumibilmente nella forma assunta dal primo strumento di gioco d'azzardo: gli astragali avevano forme talmente diverse tra loro che l'elevata arbitrarietà dei risultati ottenibili con i lanci non permise di evidenziare alcun tipo di regolarità meritevole di considerazione da parte dei matematici.

Giordano e Galileo

I primi e documentati studi condotti nel campo delle probabilità risalgono al XVI secolo e sono riportati nel libro De ludo aleae, scritto da Gerolamo Cardano intorno al 1525 e pubblicato postumo nel 1663. Geniale fisico e matematico nonché illustre medico, Cardano fu anche un cultore di astrologia e, soprattutto, un accanito giocatore d'azzardo. Tale passione lo portò a dilapidare ingenti fortune; per questo, nonostante gli elevati guadagni ottenuti con intense e molteplici attività, condusse sempre una vita estremamente modesta. Più distaccato, ma non meno prezioso, fu il contributo apportato da Galileo Galilei con il trattato "Sopra le scoperte dei dadi", pubblicato intorno al 1630. Galileo fu spinto ad occuparsi di simili "frivolezze" dal desiderio di fornire una risposta scientifica a una serie di quesiti sottopostigli da alcuni gentiluomini fiorentini, appassionati giocatori della "Zara" (un gioco con tre dadi). Uno degli interrogativi, al quale invano si era cercato di rispondere, riguardava il motivo della maggiore frequenza nelle uscite del 10 e dell'11 rispetto al 9 o al 12, nonostante fosse lo stesso il numero delle combinazioni necessarie per ottenerli. Galileo rispose che, in realtà, analizzando tutti i possibili punteggi ottenibili con il lancio di tre dadi, sia il 10 che l'11 possono ricavarsi in ventisette modi diversi, mentre il 9 e il 12 in soli venticinque.

Da Pascal a Maxwell

Qualche anno più tardi, nel 1654, il cortigiano Chevaliere de Méré chiese allo scienziato francese Blaise Pascal se fosse conveniente scommettere alla pari l'uscita di un doppio 6 su ventiquattro tiri, lanciando due dadi alla volta. Era credenza diffusa, infatti, che un gioco del genere fosse equo già sulla distanza di soli 18 tiri (essendo trentasei i diversi punteggi ottenibili dal lancio di due dadi); l'esperienza, però, contrastava in parte con tale ipotesi. Determinando esattamente quanti erano i casi possibili e quanti quelli favorevoli, Pascal calcolò che la probabilità di vincere una scommessa del genere era del quarantanove e non del cinquanta per cento. Da questi studi trasse spunto per elaborare i primi concetti del calcolo combinatorio che rese pubblici, nel 1654, nel "Traitè du triangle arithmétique". Pascal non riuscì invece a rispondere in modo del tutto soddisfacente a un altro quesito postogli da Chevaliere de Méré, su quale dovesse essere la cifra equa da pagare a un giocatore per subentrargli in una data puntata. Il problema fu risolto tre anni dopo, nel 1657, dal fisico e astronomo olandese Christiaan Huygens, che in quell'occasione formulò per la prima volta il concetto di "rendimento" o "speranza matematica". Lo sviluppo di una vera e propria teoria organica e non intuitiva delle leggi empiriche del caso richiese ancora parecchi anni di studio. Determinante a questo proposito fu l'opera dello scienziato svizzero Jakob Bernoulli, pubblicata postuma nel 1713 con il titolo "Ars conjectandi", contenente le basi del calcolo combinatorio. La prima rigorosa e moderna sistemazione della nuova scienza del calcolo delle probabilità fu però compiuta un secolo dopo, nel 1812, dal matematico francese Pierre Simon de Laplace, con il suo trattato "Théorie analytique des probabilités". Ma fu soprattutto in seguito alle ricerche del fisico scozzese James Clerk Maxwell che questa teoria iniziò intorno alla metà dell'Ottocento a trovare applicazioni in altri ampi della scienza, acquisendo spessore e rilevanza dal punto di vista scientifico. Negli stessi anni conobbero un grande sviluppo anche gli studi di statistica, la scienza che analizzando l'insieme di dati raccolti su un determinato fenomeno ne descrive l'evolversi, delineando una legge matematica che lo governa.

Il contributo di Bruno de Finetti

E' da sottolineare come nel corso di oltre tre secoli lo studio della teoria delle probabilità sia riuscito a svilupparsi in modo considerevole nonostante l'assenza di una definizione convincente e non ambigua del concetto stesso di probabilità. Infatti, secondo la definizione più antica, detta "classica", la probabilità che un evento si verifichi corrisponde al rapporto tra il numero dei casi favorevoli e il numero di tutti i casi possibili, sottintendendo che questi ultimi debbano essere tutti "ugualmente probabili". Come si può notare, questa definizione necessita della preesistenza di un concetto di probabilità; dal punto di vista matematico non è però accettabile che un'affermazione si basi sullo stesso concetto che dovrebbe descrivere. In base a una definizione più pragmatica, detta "frequentistica", la probabilità di un evento è data dalla frequenza dei risultati positivi ottenibile in una successione di prove effettuate nelle stesse condizioni; essa, però, presenta il difetto di non essere operativa nell'analisi di eventi non ancora verificatisi. A partire dal 1970, il matematico italiano Bruno De Finetti ha contribuito a dare al concetto di probabilità un significato più sostanziale e concreto. Secondo la definizione da lui proposta, detta "soggettiva", la probabilità di un evento è il grado di fiducia (variabile da soggetto a soggetto) riposta nel verificarsi del fatto stesso. Secondo questa rivoluzionaria impostazione, la probabilità non dipende più dai fattori che regolano il verificarsi di un determinato evento, ma piuttosto da una personale valutazione delle loro implicazioni. Il concetto espresso da De Finetti consente tra l'altro di utilizzare i risultati legati alle altre due definizioni (classica e frequentistica), adottandoli in base a una scelta soggettiva (senza entrare in contraddizione, quindi, con la definizione assunta). E' bene precisare, comunque, che l'attribuzione soggettiva delle probabilità non deve essere confusa con un'assoluta arbitrarietà di scelta; perché possa essere funzionale infatti, la valutazione personale deve essere espressa nel modo più equo e coerente possibile.

LA PROBABILITÀ NELLA CONCEZIONE CLASSICA

Consideriamo i se 343h79d guenti problemi.

Se lanciamo una moneta regolare e chiediamo a qualsiasi persona qual è la probabilità di ottenere testa, si ha la risposta: Nel 50% dei casi si presenta "testa", nell'altro 50% si presenta "croce".Si preferisce affermare che la probabilità di avere testa è ½.

Estraiamo a caso una carta da un mazzo di 40 carte (dopo averle ben mescolate) e chiediamo d'indicare la probabilità che la carta estratta sia di fiori. Il nostro interlocutore sapendo che delle 40 carte, 10 sono di fiori, dirà: La probabilità di estrarre una carta di fiori è del 25%, o, meglio, 10/40=1/4

Da questi due semplici esempi si può vedere che è spontanea la seguente definizione, data da Laplace, di probabilità secondo la concezione classica:

La probabilità P (E) di un evento E è il rapporto fra il numero m dei casi favorevoli (al verificarsi di E) e il numero n dei casi possibili, giudicati egualmente possibili.

La probabilità è un numero razionale p compreso fra 0 e 1:

0 ≤p ≤ 1

Il numeratore m è il numero dei casi favorevoli al verificarsi dell'evento e quindi è minore, o al più eguale, al numero n di tutti i casi possibili, che è al denominatore. In particolare:

se m=0, ossia se non esistono casi favorevoli al verificarsi dell'evento, l'evento è detto impossibile e la sua probabilità è nulla: P (E) =0;

se m=n, ossia se tutti i casi sono favorevoli al verificarsi dell'evento, l'evento è detto certo e la sua probabilità è 1: P(E)=1.

La caratteristica essenziale della concezione classica (e uno dei suoi punti deboli) è la condizione che tutti i casi in cui può manifestarsi il fenomeno siano egualmente possibili. Così, ad esempio, nel lancio della moneta le due facce devono avere eguale possibilità di presentarsi e anche nel lancio di un dado le facce devono presentarsi pari facilitate. Inoltre si deve rilevare che la definizione si può applicare quando l'insieme dei casi è un insieme finito. La definizione classica di probabilità è stata molto criticata, poiché supporre che i casi siano egualmente possibili significa supporre che abbiano eguale probabilità di verificarsi e quindi nella definizione si utilizza lo stesso concetto che si vuole definire. Per superare la circolarità della definizione già J. Bernoulli aveva introdotto il principio della ragione non sufficiente detto, successivamente, principio d'indifferenza. Tale principio asserisce che, in mancanza di ragioni che permettano di assegnare probabilità diverse a ciascuno degli eventi elementari, questi devono essere considerati come egualmente possibili. Ad esempio, se non ci sono motivi per affermare che un dado sia irregolare, si accetta che ogni faccia sia equipossibile. Un altro tipo di difficoltà s'incontra nel calcolo del numero dei casi possibili e dei casi favorevoli quando i casi sono molto numerosi; tale calcolo è addirittura impossibile se si debbono valutare insiemi infiniti. Inoltre il campo di applicazione della probabilità definita nel modo classico risulta molto ristretto perché la definizione è valida per eventi nei quali vi siano ragioni di simmetria che permettano di giudicare egualmente possibili i vari casi (come nel lancio di una moneta o di un dado non truccati, nell'estrazione dei numeri del lotto e, in generale nei problemi riconducibili a estrazione a sorte di palline da un'urna). Se non vi sono ragioni per ammettere che un caso sia più favorito di un altro, si accetta l'impostazione classica che è utile per quei problemi che ammettono come modello matematico un'urna contenente palline eguali per forma e peso, ma distinguibili per il colore. Tipico esempio di applicazione della concezione classica di probabilità si ha in genetica con le leggi ottenute da Mendel (verificate statisticamente da Mendel e da altri biologi ) nello studio dei problemi legati all'ereditarietà. Altro campo di applicazione della concezione classica della probabilità si ha nella teoria del campionamento. Nell'impostazione classica non si può determinare la probabilità di molti eventi, ad esempio, la probabilità per una persona di 40 anni di raggiungere l'età di 60 anni, la probabilità di subire un furto, la probabilità che un nuovo medicinale dia esiti positivi nella cura di una malattia. È necessario quindi rivedere e modificare la definizione di Laplace per ampliare il campo di applicazione della probabilità.

LA PROBABILITÀ NELLA CONCEZIONE FREQUENTISTA

Dalle critiche alla definizione classica di probabilità, anche in conseguenza dei progressi delle scienze sperimentali, si sviluppò una nuova concezione della probabilità: la concezione frequentista, che si può applicare quando si possono eseguire tante prove quante si vogliono sull'evento, oppure sono disponibili tavole con i risultati di rilevazioni statistiche relative a un certo fenomeno (ad esempio, le tavole di mortalità e di sopravvivenza). Secondo la concezione frequentista, per conoscere la probabilità di un evento si deve ricorrere all'esperimento. È importante rilevare che per un frequentista non ha senso calcolare la probabilità di una singola prova, perché non si può prevedere il risultato di un singolo esperimento, mentre in una gran successione di prove si riscontra una sorprendente regolarità. Ad esempio, se si lancia più volte una moneta non si può calcolare la probabilità che a un determinato lancio si presenti testa, ma solo la probabilità che si presenti testa dopo avere effettuato un numero sufficientemente grande di lanci. La concezione frequentista è basata sulla definizione di frequenza relativa di un evento.

Si definisce frequenza relativa di un evento in n prove effettuate nelle stesse condizioni, il rapporto fra il numero k delle prove nelle quali l'evento si è verificato e il numero n delle prove effettuate:

,

0 ≤p ≤ 1

La frequenza dipende non solo da n, numero delle prove fatte, ma, per uno stesso n, può variare al variare del gruppo delle prove, cioè se, per esempio, si lancia 100 volte una moneta e si presenta testa 46 volte, effettuando altri 100 lanci, testa si può presentare un altro numero di volte, ad esempio 52; ne segue che la frequenza per il primo gruppo di lanci è 46/100, per il secondo è 52/100. Anche la frequenza è compresa fra 0 e 1, ma se f=0 non si può affermare che l'evento è impossibile, ma che non si è verificato in quelle n prove; e se invece f=1 non si può affermare che l'evento è certo, ma che in quelle n prove esso si è sempre verificato. La frequenza varia al variare del gruppo delle prove eseguite, ma, fatto interessante, è stato costatato che se il numero di prove è sufficientemente alto, il rapporto k/n tende a stabilizzarsi. Questo fatto era già stato costatato da alcuni demografi nel diciassettesimo e diciottesimo secolo su fenomeni quali frequenze di nascite maschili e frequenze di decessi in una stessa popolazione. Inoltre, per fenomeni di cui è possibile calcolare la probabilità con la concezione classica, la frequenza, al crescere delle prove, tende, generalmente, ad avvicinarsi alla probabilità calcolata a priori. A questo riguardo sono storici gli esperimenti di Buffon e Pearson. Il primo lanciò 4.040 volte una moneta ottenendo testa 2.048 volte con una frequenza 0,5069. Il Pearson in un primo esperimento con 12.000 lanci ottenne testa 6.019 volte, con frequenza 0,50158; in un secondo esperimento ottenne, su 24.000 lanci, 12.012 volte testa, con frequenza 0,5005. Quindi la frequenza, al crescere del numero delle prove, si avvicina ordinariamente al valore 0,5 della probabilità dell'evento viene testa, calcolato con l'impostazione classica. Si giunge a enunciare, per eventi per i quali si può calcolare la probabilità, la cosiddetta

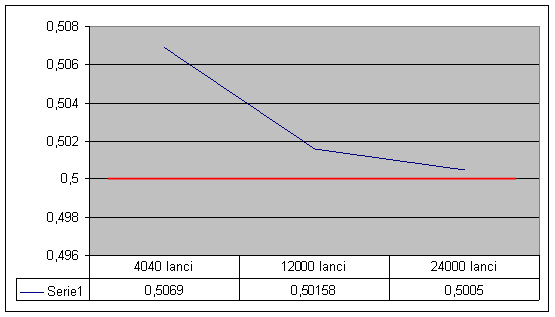
Figura 1: la linea blu rappresenta la frequenza delle volte in cui si è ottenuto testa. La linea rossa la frequenza calcolata a priori. All'aumentare dei lanci, la frequenza ottenuta empiricamente si avvicina a quella calcolata a priori.

legge empirica del caso: in una serie di prove, ripetute un gran numero di volte, eseguite tutte nelle stesse condizioni, la frequenza tende ad assumere valori prossimi alla probabilità dell'evento e, generalmente, l'approssimazione è tanto maggiore quanto più numerose sono le prove eseguite.

Bisogna applicare con attenzione tale legge, in quanto la legge afferma che se si eseguono numerose prove su un evento, la frequenza ordinariamente si discosta di poco dalla probabilità, ma ciò non esclude che qualche volta, anche se raramente, la frequenza, che è un valore sperimentale, assuma valori non attesi. Inoltre non è detto che, se, ad esempio, nel gioco del lotto un numero non si è presentato da molte settimane, abbia maggiore probabilità di presentarsi, in quanto per ogni estrazione tale probabilità è sempre la stessa, indipendentemente dai numeri usciti nelle altre estrazioni. La legge empirica del caso permette di formulare la seguente definizione frequentista di probabilità per eventi ripetibili.

La probabilità di un evento è la frequenza relativa in un numero di prove ritenuto sufficientemente elevato.

In generale non si può dire quante prove siano necessarie, perché il numero delle prove dipende dal fenomeno in esame. La frequenza, calcolata in un gran numero di prove, permette di prevedere i risultati di prove future eseguite nelle stesse condizioni. Il campo di applicazione della concezione frequentista è molto vasto, in quanto la definizione può essere applicata a fenomeni dei quali si posseggano dati statistici riguardanti fenomeni passati che si sono verificati in condizioni analoghe. Ad esempio, si potranno calcolare, per una data popolazione, la probabilità di morte o di sopravvivenza degli individui o la probabilità di nascita di maschi o di femmine. Si hanno pure importanti applicazioni nella medicina, nella psicologia, nell'economia, nella meccanica quantistica e, in generale, in tutte le scienze per le quali si possono utilizzare metodi statistici. Le probabilità calcolate sia con la concezione classica, sia con la concezione frequentista, sono dette probabilità oggettive per distinguerle dalle probabilità valutate secondo la concezione soggettiva.

LA PROBABILITÀ NELLA CONCEZIONE SOGGETTIVA (O PERSONALE)

Esaminiamo i seguenti problemi.

Qual è la probabilità per uno studente di trovare impiego subito dopo il conseguimento del diploma?

Domenica prossima si svolgerà un'importante maratona internazionale; qual è la probabilità che la gara sia vinta da Pini?

Qual è la probabilità che un nuovo modello di automobile ha d'incontrare il favore del pubblico?

Per eventi del tipo indicato non è possibile valutare la probabilità né secondo la concezione classica, perché non si possono determinare i casi possibili e i casi favorevoli, né secondo la concezione frequentista, perché gli eventi non sono ripetibili; in questi casi si stima la probabilità in base allo stato d'informazione, precisamente:

La probabilità P(E) di un evento E è la misura del grado di fiducia che un individuo attribuisce, in base alle sue informazioni e alle sue opinioni, al verificarsi dell'evento E.

Le valutazioni di probabilità sono soggettive, ossia possono variare da individuo a individuo, ma deve essere rispettata la coerenza. Per meglio fissare questo concetto, B. de Finetti, che è uno dei principali sostenitori di quest'impostazione si ricollega alle scommesse e dà la seguente definizione:

La probabilità di un evento E, secondo l'opinione di un certo individuo, è il prezzo p che ritiene equo attribuire all'importo unitario, esigibile al verificarsi di E.

Ossia la probabilità è quella somma p che l'individuo è disposto a pagare per ricevere una lira nel caso si verifichi E; ma, per coerenza, egli è anche disposto ad accettare la scommessa inversa, ossia a ricevere p e pagare una lira al verificarsi di E. Ad esempio, attribuire la probabilità di 0,7 a un certo evento E significa essere disposti a pagare 70 lire per riceverne 100 nel caso si verifichi l'evento E; e inversamente, per coerenza, essere disposti a ricevere 70 lire e pagarne 100 nel caso si verifichi l'evento E. In questa concezione la probabilità è un numero reale compreso fra 0 e 1. Infatti: se l'evento è giudicato impossibile, il prezzo è p=0, se l'evento è giudicato certo, il prezzo è p=1; in tutti gli altri casi 0<p<1. Il campo di applicazione di questa concezione è illimitato in quanto qualsiasi evento può essere valutato in base a essa; anzi, anche inconsciamente, quando prendiamo qualche decisione, il fatto stesso di scegliere un'alternativa invece di un'altra, presuppone che abbiamo assegnato delle probabilità. Riprendiamo in esame i problemi indicati all'inizio.

La valutazione della probabilità di trovare impiego per uno studente neodiplomato dipende da molti fattori, come, ad esempio, la sua preparazione professionale, le sue doti intellettuali, la sua capacità di rapporti interpersonali. La valutazione della probabilità è puramente soggettiva e persone diverse possono assegnare a uno stesso giovane probabilità diverse. Ad esempio, una persona pessimista può valutare che la probabilità di trovare lavoro sia del 25%, un'ottimista, invece, può assegnare la probabilità del 70%. Entrambe le valutazioni, pur così diverse, devono essere accettate, purché siano coerenti.

La probabilità che un campione vinca una gara dipende da vari fattori, quali le sue condizioni di forma o la presenza di altri atleti di maggiore capacità. Anche in questo caso in base alle informazioni e alle opinioni, le valutazioni della probabilità di vittoria sono generalmente diverse secondo lo sportivo o il giornalista che lo formula.

Anche per quanto si riferisce al successo di un prodotto nuovo presso gli acquirenti, le opinioni dipendono dai gusti di chi compie la valutazione e anche dalla sua stima per la Casa produttrice.

Ad esempio, un imprenditore può assegnare una valutazione prudenziale del 40% al successo di un nuovo modello di automobile, un altro imprenditore, che ama il rischio, con le stesse informazioni può attribuire al nuovo modello di automobile la probabilità del 70% di successo. In base a queste valutazioni si possono prendere decisioni diverse: l'imprenditore prudente può stimare rischioso produrre il nuovo modello e non dà corso alla produzione, mentre l'imprenditore più ottimista decide, in base alla sua valutazione, d'iniziare la produzione del nuovo modello. A quest'impostazione sono state mosse critiche poiché le valutazioni di probabilità verrebbero, in generale, a differire da individuo a individuo.

LA PROBABILITÀ NELL'IMPOSTAZIONE ASSIOMATICA

Con lo sviluppo degli studi matematici, soprattutto con l'applicazione della logica formale all'analisi dei fondamenti della matematica e della scienza in genere, si è giunti a un'impostazione che dà della probabilità una definizione implicita mediante un sistema di assiomi, analogamente, per esempio, alla definizione implicita di retta data dalla Geometria razionale. L'impostazione assiomatica è sorta proprio per l'esigenza dei matematici di sistemare in modo rigoroso le conoscenze e le molte applicazioni del calcolo delle probabilità che durante due secoli i ricercatori hanno sviluppato in molteplici campi. L'idea di costruire un'impostazione assiomatica si può far risalire, per lo meno, a H. Poincarè (Calcul des probabilités, 1894). Successivamente molti autori hanno proposto varie assiomatiche; citiamo, fra i molti, A. N. Kolmogoroff (Grundbegriffe der Wahrscheinlichkeitsrechnung, 1933) e D. Scott-P. Krauss (in Assigning probabilities to logical formula, Aspect of introductive logic, a cura di Hintikka e Suppes, 1966). A ogni eperimento (reale o concettuale ) si può associare un insieme U, detto universo o spazio dei campioni o spazio degli eventi, i cui elementi sono tutti i possibili risultati dell'esperimento (o fenomeno). La scelta dell'universo U, legato a un certo esperimento, non è fissa, ma può dipendere dal problema. Ad esempio, se lanciamo un dado e vogliamo distinguere i risultati possibili, possiamo considerare come insieme universo l'insieme U= ; se, invece, c'interessa solo distinguere i numeri pari dai numeri dispari, possiamo assumere come insieme universo l'insieme U' costituito dagli elementi P e D: U'= . Precisiamo alcune caratteristiche del concetto di evento:

La nozione di evento è assunta come primitiva.

Un evento(passato, o presente, o futuro) è descrivibile con un'espressione linguistica alla quale si può associare un sottoinsieme dell'insieme universo U.

Si può identificare l'evento con il sottoinsieme associato all'espressione linguistica che lo descrive e tradurre le operazioni logiche sugli eventi in operazioni fra sottoinsiemi.

I sottoinsiemi costituiti da un solo elemento sono detti eventi elementari.

Si dirà che l'evento si verifica se il risultato dell'esperimento è un elemento appartenente al sottoinsieme associato all'evento. Ad esempio, nel lancio di un dado, l'evento <<la faccia presentata è un numero pari>>, risulta verificato se si presenta una delle facce 2, 4, 6. Sugli eventi si definiscono operazioni analoghe a quelle definite sugli insiemi.

Si definisce evento contrario dell'evento A, l'evento A che si verifica se e solo se non si verifica A, cioè A è il sottoinsieme complementare di A rispetto a U.

Si definisce somma logica (o unione) di due eventi A e B, l'evento A È B che si verifica quando si verifica almeno uno degli eventi A o B.

Si definisce prodotto logico (o intersezione) di due eventi A e B, l'evento A B che si verifica se si verificano entrambi gli eventi A e B.

In particolare:

Due eventi si dicono incompatibili se il verificarsi dell'uno esclude il verificarsi dell'altro, cioè se i loro sottoinsiemi sono disgiunti: A B=

L'evento impossibile corrisponde al sottoinsieme vuoto;

L'evento certo corrisponde all'insieme U.

L'insieme degli eventi, nel caso che U sia un insieme finito, è l'insieme formato da tutti i sottoinsiemi di U, e quindi è l'insieme delle parti P (U). Dato un universo U consideriamo una famiglia F di sottoinsiemi di U (non necessariamente coincide con P (U)), che goda delle seguenti proprietà:

Contenga U come suo elemento;

Sia chiusa rispetto alle operazioni di unione, intersezione e complementazione (ossia tale che se contiene due sottoinsiemi A e B di U contenga la loro unione, la loro intersezione e i loro complementari).

Si deduce che in F vi è anche l'insieme vuoto che è il complementare di U. Gli elementi di F sono detti eventi casuali. In tali ipotesi F è detta campo degli eventi (o s -algebra). Si ha la seguente definizione assiomatica di probabilità:

La probabilità P(E)è una funzione che associa a ogni evento del campo degli eventi un numero reale, in modo che siano soddisfatti i seguenti assiomi:

P(E) >= 0

P(U) = 1

Se E₁ e E₂ sono incompatibili, ossia E₁ E ,si ha: P(E₁ U E ) = P(E₁) + P(E₂).

Da questi assiomi si deducono le seguenti proprietà:

a) L'evento impossibile ha probabilità zero. Infatti dall'eguaglianza:

U = U U Ø

applicando l'assioma 3° si ricava:

P(U) = P(U U Ø) = P(U) + P(

e per l'assioma 2° si ha:

1 = 1 + P(

da cui segue:

P(

b) Dato un evento E, la probabilità dell'evento contrario è eguale al complemento a 1 della probabilità dell'evento E, in pratica:

P() = 1 - P(E)

Infatti, dalla relazione:

U = E È

segue, per l'assioma 3°:

P(U) = P(E U ) = P(E) + P()

ed essendo, per l'assioma 2°, P(U) = 1, si ha:

P() = 1 - P(E)

c) Dalla relazione precedente e dall'assioma 1° si deduce che la probabilità è un numero reale compreso fra zero e uno, cioè:

0<= P(E) <=1

d) Per la proprietà associativa dell'unione fra insiemi, si ha;

P(E₁ U E₂ U E₃) = P(E₁)+ P(E₂)+ P(E₃)

purché:

E₁ E₂ = E₁ E₃ = E₂ E₃ =

cioè se gli eventi sono incompatibili a due a due. La proprietà si estende a K eventi a due a due incompatibili:

P(E₁ U  E_{2 È} U E₃.U E_k )= P(E₁)+ P(E₂)+ P(E₃)+.+ P(E_k)

se:

E_i E_j =   ; i ¹ j; i , j=1,2,.,k

e) Siano E₁ ,., E_n eventi elementari di U, incompatibili a due a due e aventi come unione l'insieme U, cioè:

E_i E_j = ; i ¹ j; i , j=1,2,.,n

E₁  U E₂  U U  E_n=U

Allora, per la proprietà d) e per l'assioma 2°, si ha:

P(E₁ U E₂  .È E_n )= P(E₁)+ P(E₂)+.+ P(E_n)=P(U)=1

Se si aggiunge l'ipotesi che gli eventi siano equiprobabili, come nell'impostazione classica, ciascun evento avrà probabilità;

i=1,2,.,n

Se E è un evento unione di m eventi elementari, la sua probabilità è allora:

Si può quindi affermare che:

La probabilità secondo la concezione classica è un caso particolare della probabilità secondo l'impostazione assiomatica.

f) Se E₁ < E₂ allora la probabilità della differenza fra E₂ ed E₁ è uguale alla differenza delle probabilità :

P(E₂ - E₁)=P(E₂)- P(E₁)

Infatti, essendo E₁ ed E₂ - E₁ disgiunti, si può scrivere (vedi figura):

E₂ = E₁ U (E₂ - E₁)

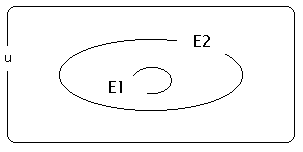
E per l'assioma 3°:

P(E₂)=P(E₁) + P(E₂ - E₁)

cioè:

P(E₂ - E₁)=P(E₂)- P(E₁)

L'impostazione assiomatica è soddisfacente dal punto di vista teorico, ma non indica come valutare la probabilità di un evento, poiché rimane da definire il tipo di funzione.

PROBABILITÀ DELLA SOMMA DI EVENTI

La probabilità della somma logica di eventi, se gli eventi sono incompatibili, è espressa dall'assioma 3° e dalla sua estensione a più di due eventi incompatibili a due a due, come si è visto nella proprietà d). Si presenta il problema di calcolare la probabilità della somma logica in caso di eventi compatibili. Esaminiamo alcuni casi.

a) Se due eventi A e B sono compatibili si ha la seguente relazione di Boole:

P(A U B)=P(A) + P(B) - P(A B)

cioè:

La probabilità della somma logica di due eventi è eguale alla somma delle probabilità dei due eventi diminuita della probabilità dell'intersezione dei due eventi.

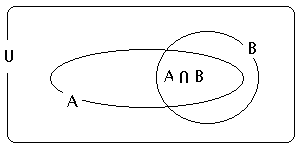
Infatti essendo A e (B - A) disgiunti si può scrivere:

A U B = A U (B - A)

e inoltre

B - A = B - (A B) dove (A B) < B

Applicando il 3° assioma e la sua proprietà f) si ottiene:

P(A U B) = P(A) + P(B - A) = P(A) + P[B - (A B)] = P(A) + P(B) - P(A B)

b) La precedente relazione si estende alla somma logica di tre eventi A, B, C qualunque (se i tre eventi fossero incompatibili a due a due, ritroveremmo la proprietà d)):

P(A U B U  C) = P(A) + P(B) + P(C) - P(A B) - P(A C) - P(B C) + P(A B C)

Una verifica intuitiva si può avere esaminando i sottoinsiemi A,B,C, nel seguente grafico:

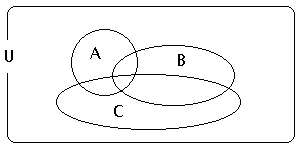
La precedente relazione può essere estesa a un numero qualunque di eventi.

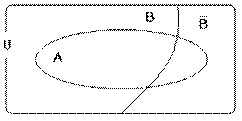
c) Se A e B sono due eventi qualunque si ha la relazione:

Infatti, i due eventi B e sono incompatibili e la loro unione è U; per le proprietà delle operazioni fra insiemi si può scrivere:

I due sottoinsiemi e sono disgiunti poiché lo sono B e ; quindi, per l'assioma 3° si ha la tesi, considerando il primo e l'ultimo membro delle eguaglianze precedenti:

d) Si può estendere la precedente relazione.

Se B₁,B₂,.,B_K costituiscono una partizione di U, ossia se:

B_{i¹ Æ} , i=1,.k, cioè nessun B_i è l'evento impossibile;

B_i B_j i¹ j, i,j=1,.,k, cioè B_i è incompatibile con tutti gli altri;

B UB U U  B_k=U, ossia la somma logica di tutti i B_i è l'evento certo;

allora, si ha la relazione:

La partizione è anche detta classe completa di eventi incompatibili. Talvolta per il calcolo della probabilità di un evento A è più facile servirsi della probabilità dell'evento contrario e applicare la proprietà b), che si può scrivere nella forma:

PROBABILITÀ CONDIZIONATA. EVENTI DIPENDENTI E INDIPEN-DENTI

Si è detto più volte che la valutazione di probabilità dipende anche dallo stato d'informazione, quindi la probabilità di un evento può variare subordinatamente al verificarsi di un altro evento. Ad esempio, nel lancio di un dado, la probabilità che esca il 4 è 1/6. Se si ha l'informazione che è uscito un numero pari, la probabilità che sia 4 è 1/3, mentre se l'informazione fosse che è uscito un numero superiore a due, la probabilità sarebbe 1/4.

Si definisce probabilità di un evento A condizionata (o subordinata) all'evento B, e s'indica P(A/B), la probabilità del verificarsi di A nell'ipotesi che B si sia verificato. Se B non si verifica, l'evento A/B non è definito.

Facciamo notare che per valutare P(A) si è preso in considerazione l'universo U degli eventi elementari(o dei casi possibili nell'impostazione classica); adesso, per ulteriori informazioni o per effetto di scelta, l'universo U si riduce al suo sottoinsieme B e quindi è in B che si debbono considerare gli eventi elementari. In sostanza, si valuta la probabilità di A subordinata all'ipotesi B, mentre prima si valutava la probabilità di A subordinata all'ipotesi U; l'informazione restringe l'universo U a un suo sottoinsieme B.

Secondo l'impostazione classica si vede facilmente che se b sono i casi favorevoli al verificarsi dell'evento B, e k sono quelli favorevoli al verificarsi di A B, la probabilità di A condizionato a B risulta:

La precedente frazione si può trasformare dividendo per n, numero totale dei casi possibili, il numeratore e il denominatore, e si ottiene:

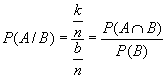
L'impostazione assiomatica definisce proprio come probabilità di A condizionata a B la relazione:

Si può dimostrare, che la P(A/B), definita dalla precedente, soddisfa ai tre assiomi dell'impostazione assiomatica enunciati precedentemente. Osserviamo che P(A/B) può essere minore, eguale, maggiore di P(A). Analogamente si può calcolare la probabilità di B condizionata ad A:

La probabilità di A condizionata a B può essere eguale, o maggiore o minore di P(A). Importante è il caso in cui vale l'eguaglianza; precisamente si ha la seguente definizione:

Due eventi A e B si dicono stocasticamente indipendenti (ossia indipendenti dal punto di vista del calcolo delle probabilità), se:

Se questa relazione è vera, si deduce, con alcuni passaggi, che risulta pure P(B)=P(B/A). La relazione d'indipendenza stocastica è simmetrica, cioè se A è indipendente da B, anche B è indipendente da A. Se non vale l'eguaglianza precedente, gli eventi si dicono stocasticamente dipendenti; si hanno i due seguenti casi:

Se risulta P(A/B)>P(A), si dice che gli eventi sono correlati positivamente, cioè l'informazione ha aumentato la probabilità dell'evento A;

Se risulta P(A/B)<P(A), si dice che gli eventi sono correlati negativamente, cioè l'informazione ha diminuito la probabilità dell'evento A.

PROBABILITÀ DEL PRODOTTO LOGICO DI EVENTI

Dati due eventi, si definisce evento composto o prodotto logico degli eventi, l'evento che risulta verificato se gli eventi componenti si verificano entrambi. Nella rappresentazione insiemistica all'evento composto è associato il sottoinsieme intersezione degli eventi componenti.

Dalle relazioni sulle probabilità condizionate si ricava immediatamente:

oppure

Queste due relazioni costituiscono il teorema delle probabilità composte.

La probabilità dell'evento composto, o del prodotto logico A B, è uguale al prodotto della probabilità di un evento per la probabilità dell'altro condizionata al verificarsi del primo.

Se gli eventi sono stocasticamente indipendenti, cioè se P(A / B) = P(A), oppure se P(B / A) = P( B ), il teorema delle probabilità composte diventa:

Il teorema delle probabilità composte si può estendere al prodotto logico di tre o più eventi. Se gli eventi E₁, E₂,.,E_n sono stocasticamente indipendenti, la probabilità del loro prodotto logico è uguale al prodotto delle probabilità dei singoli eventi. Se gli eventi E₁, E₂,.,E_n sono stocasticamente dipendenti, la probabilità del loro prodotto logico è eguale al prodotto della probabilità del primo per la probabilità del secondo condizionata al primo, per la probabilità del terzo condizionata ai primi due, eccetera.

PROBABILITÀ COMPLETA O TOTALE

Sia data una partizione dell'evento certo in n eventi non impossibili, incompatibili a due a due e tali che la loro somma logica sia l'evento certo e si consideri un evento A. Mediante la seguente rappresentazione grafica visualizziamo quest'ipotesi:

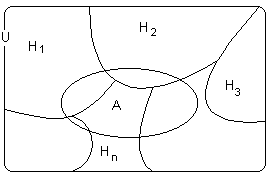
Vogliamo esprimere la probabilità di A mediante la probabilità degli eventi Hi. Dallo schema si rileva che il sottoinsieme A è l'unione delle intersezioni di A con gli Hi che sono disgiunti; la probabilità di A è, allora, la somma delle probabilità degli eventi AÇ Hi:

Applicando il teorema delle probabilità composte si ricava:

La formula trovata per P(A) è detta formula della probabilità totale o completa (detta da alcuni autori, formula di disintegrazione). Questa formula permette di calcolare la probabilità di un evento A somma logica di n eventi incompatibili a due a due, eventi che sono ognuno prodotto logico di due eventi. Tale formula trova un'interessante applicazione nel teorema di Bayes.

PROBLEMA DELLE PROVE RIPETUTE (O SCHEMA DI BERNOULLI)

In molti problemi di applicazione si debbono considerare le prove indipendenti ripetute di un esperimento. Per ogni prova sia p la probabilità che la prova dia esito positivo (o successo, come si usa dire) e sia q=1-p la probabilità contraria (o fallimento). Vogliamo calcolare la probabilità che su n prove indipendenti, k e solo k abbiano successo. Supponiamo che l'esperimento abbia successo nelle prime k prove e fallimento nelle successive n-k. Per il principio delle probabilità composte, la probabilità di quest'evento è data da:

Le k prove con successo possono presentarsi con ordine diverso, ma, ovviamente, la probabilità ha lo stesso valore precedente. Il numero degli eventi formati da k successi e da n-k fallimenti è dato da tutte le combinazioni delle n prove a k a k e quindi è .

La probabilità che, su n prove bernoulliane, k e solo k abbiano successo è data da:

TEOREMA DI BAYES

Una prima formulazione del teorema di Bayes (o teorema della probabilità delle cause) si ricava dal teorema delle probabilità composte. Consideriamo le relazioni e indicando gli eventi con A e H, come si usa scrivere in questo contesto:

Dall'eguaglianza dei due secondi membri si ottiene la seguente relazione che esprime il teorema di Bayes nel caso di un solo evento H:

In generale, se un evento A può verificarsi in seguito a più cause, che si escludano a vicenda, dalla conoscenza della probabilità delle cause, essendosi verificato l'evento A, possiamo calcolare la probabilità che esso sia dovuto a una determinata causa. Ricaviamo adesso la forma generale del teorema di Bayes. Sappiamo che data una partizione di U e un evento qualunque A si può esprimere P(A) nel modo seguente:

e sostituendo questo valore di P(A) si ha la formula che esprime il:

Teorema di Bayes

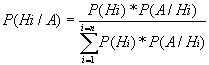
Dal teorema si rileva che le probabilità <<a posteriori>> P(H_i /A) delle cause (cioè dopo che l'evento A si è verificato), sono proporzionali alle corrispondenti probabilità <<a priori>> P(H_i) corrette con il fattore P(A/H_i). In altre parole, se è alta la probabilità che l'evento A sia effetto della causa H_i , il fatto che l'evento A si sia verificato aumenta la probabilità, anche se non dà la certezza, che a produrlo sia proprio la causa H_i . Viceversa, se è bassa la probabilità che l'evento A sia effetto della causa H_i, il fatto che l'evento A si sia verificato diminuisce la probabilità che a produrre A sia stata proprio la causa H_i. In molti problemi non si conoscono le probabilità P(H_i) delle cause; in questi casi si assume per le cause un eguale valore di probabilità. Il teorema di Bayes è interpretato dai soggettivisti come un modo per incrementare lo stato di conoscenza di un fenomeno in base alle nuove informazioni. Mendel applicò il teorema di Bayes ai suoi studi di genetica.

IL POKER E IL CALCOLO DELLE PROBABILITÀ
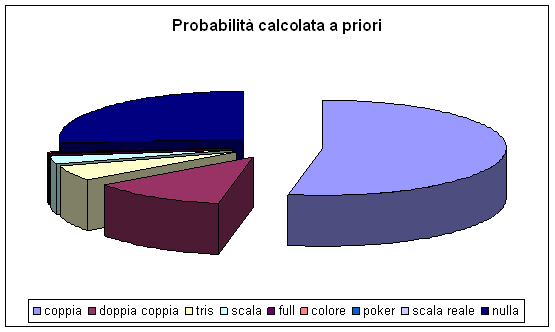
Per giocare a poker, quattro persone, hanno bisogno di un mazzo di 32 carte. Le 32 carte, hanno otto valori (7, 8, 9, 10, J, Q, K, A), nei quattro semi (quadri, cuori, picche, fiori).  Ad ogni giocatore vengono distribuite 5 carte. I punti sono :  -Coppia (2 carte dello stesso valore) -Doppia coppia (2 coppie) -Tris (3 carte dello stesso valore) -Scala semplice(5 carte di seme "diverso", in ordine) -Full (un Tris e una Coppia) -Colore (5 carte dello stesso seme, non in ordine) -Poker (4 carte dello stesso valore) -Scala reale (5 carte dello stesso seme, in ordine ) Calcoliamo, la probabilità di realizzare, le suddette combinazioni, usando la definizione classica di probabilità  P = (N° casi favorevoli ) / (N° casi possibili). Il numero dei casi possibili, sono le combinazioni delle 32 carte a gruppi di 5 : C32,5  =(32 x 31 x 30 x 29 x 28 )/5! = 201376.  Primo caso:Coppia (2 carte dello stesso valore). Esempio J J K K La prima carta può essere scelta in 32 modi, la seconda carta in 3 modi distinti. Poiché l'ordine non è importante, le possibili combinazioni saranno (32 x 3) / 2= 48. La terza carta deve essere scelta fra le rimanenti 7 x 4 = 28 (diverse da quelle della coppia), la quarta carta deve essere scelta fra le rimanenti 6 x 4 = 24 (diverse da quelle della coppia e dalla terza), la quinta carta deve essere scelta fra le rimanenti 5 x 4 = 20 (diverse da quelle della coppia, dalla terza e dalla quarta) Le possibili combinazioni delle tre carte, poiché l'ordine non conta, saranno: (28 x 24 x 20 ) / 3!=2240 Il numero delle possibili coppie è dato da: 48 x 2240 =107520. La probabilità di fare una coppia è: P = (N°casi favorevoli ) / (N° casi possibili) =107520/201376 =480/899 = 53% circa  Secondo  caso: Doppia Coppia (2 coppie). Esempio K K La prima carta può essere scelta in 32 modi, la seconda carta in 3 modi distinti. La terza carta deve essere scelta fra le rimanenti 7 x 4 = 28 (diverse da quelle della coppia), La quarta carta deve essere scelta in tre modi distinti, poiché  anche l'ordine delle due coppie non conta il numero di combinazioni che danno due coppie è: [(32 x 3 /2) x (28 x 3/2 )] /2 = 1008 La quinta carta deve essere scelta fra le rimanenti 6 x 4 =24 (diverse da quelle delle coppie). Il numero di combinazioni che danno una doppia coppia è: 1008 x 24 =24192. La probabilità di avere una doppia coppia è: P = (N°casi favorevoli ) / (N° casi possibili) =24192/201376 =108/899 circa 12% Terzo caso: Tris (3 carte dello stesso valore). Esempio K K La prima carta può essere scelta in 32 modi, la seconda carta in 3 modi distinti, la terza in 2 modi. Poiché l'ordine non conta i possibili tris, con tre carte sono ( 32 x 3 x 2) / 3! =32. La quarta carta deve essere scelta fra le rimanenti 7 x 4 = 28 (diverse da quelle del tris). La quinta carta deve essere scelta fra le rimanenti 6 x 4 = 24 (diverse da quelle del tris e dalla quarta). Le possibili combinazioni  contenenti un tris sono [32 x (28 x 24) /2]=10752 La probabilità di fare un tris  è  P = (N°casi favorevoli ) / (N° casi possibili) =10752/201376 = 48/899 circa 5,3%  Quarto caso: Full (un Tris e una Coppia). Esempio La prima carta può essere scelta in 32 modi, la seconda carta in 3 modi distinti, la terza in 2 modi. Poiché l'ordine non conta, i possibili tris con tre carte sono: ( 32 x 3 x 2) / 3! =32. La quarta carta deve essere scelta fra le rimanenti 7 x 4 = 28 (diverse da quelle del tris). La quinta carta deve essere scelta in 3 modi distinti. Quindi i full sono 32 x (28 x 3 )/2 = 1344 La probabilità di fare un full  è P = (N°casi favorevoli ) / (N° casi possibili) =1344/201376 =6/899 circa 0,67% Quinto caso: Poker (4 carte dello stesso valore). Esempio La prima carta può essere scelta in 32 modi, la seconda carta in 3 modi distinti, la terza in 2 modi, la quarta in un solo modo. Poiché l'ordine non conta i possibili poker con quattro carte sono: ( 32 x 3 x 2 x 1) / 4! =8. La quinta carta può essere scelta in 7 x 4 = 28 modi distinti.  Quindi le possibili combinazioni sono 8 x 28 =224. La probabilità di fare un poker è : P = (N°casi favorevoli ) / (N° casi possibili) = 224/201376 = 1/899 circa 0,11% Sesto caso: Scala Reale (5 carte dello stesso seme, in ordine). Esempio  J J Q Q K K A A La prima carta può essere scelta in 5 x 4 = 20 modi, le altre carte in un solo modo. La probabilità di fare un scala reale è : P = (N°casi favorevoli ) / (N° casi possibili) =20/201376 =5/50344 = 0,01%. Settimo caso: Scala (5 carte di seme "diverso", in ordine). Esempio (scala minima) A A Esempio (scala massima) J J Q Q K K A A La prima carta può essere scelta in 5 x 4 =20 modi, la seconda carta in 4 modi distinti, la terza in 4, la quarta in 4 e la quinta in 4. Le possibili combinazioni sono: 20 x 4 x 4 x 4 x 4 = 5120  Da questo numero dobbiamo togliere le 20 scale reali. Quindi, le possibili combinazioni sono 5120-20 = 5100 La probabilità di fare un scala è : P = (N°casi favorevoli ) / (N° casi possibili) =5100/201376 =1275/50344 circa 2,5% Ottavo  caso: Colore (5 carte dello stesso seme, non in ordine). Esempio  J J Q Q K K La prima carta può essere scelta in 8 x 4 =32 modi, la seconda carta in 7 modi distinti, la terza in 6, la quarta in 5 e la quinta in 4.  Poiché l'ordine non conta, le possibili combinazioni sono (32 x 7 x 6 x 5 x 4) /5! = 224, togliendo le 20 scale reali si ottiene 224-20 = 204. La probabilità di fare un colore è : P = (N°casi favorevoli ) / (N° casi possibili) =204/201376 =51/50344 circa 0,10% In conclusione punteggio probabilità coppia doppia coppia tris scala full colore poker scala reale nulla

PROVA EMPIRICA n.1

estrazione manuale

Pescando da un mazzo di 32 carte (8 valori per 4 semi) ho cercato di verificare empiricamente i dati ottenuti con il calcolo delle probabilità precedentemente illustrato.

Riporterò qui sotto le percentuali ottenute dopo diverse ripetizioni:

Dopo 10 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

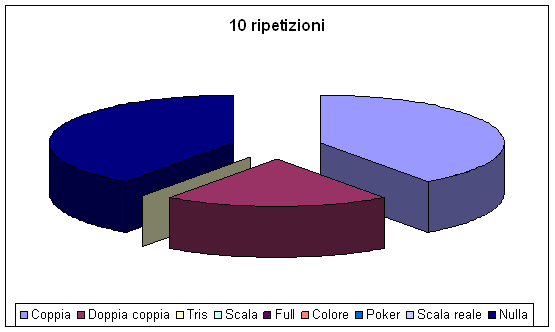
Possiamo notare come i valori siano decisamente differenti da quelli ottenuti matematicamente.

Con un basso numero di ripetizioni, il risultato ottenuto è infatti in larga parte condizionato dal caso.

Dopo 50 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

Alla 50 ripetizione i valori iniziano ad essere più simili a quelli matema-tici ma ancora eccessivamente viziati dal caso.

Dopo 100 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

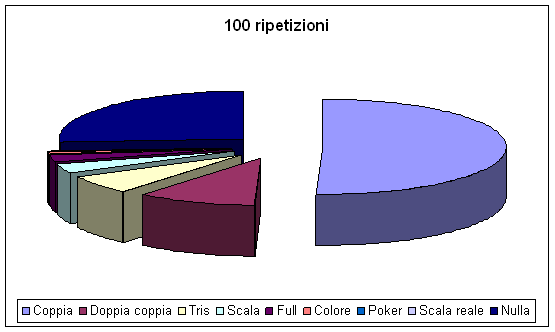
100 ripetizioni non sono ancora sufficienti. Alcuni valori tendono ad avvicinarsi a quelli matematici (probabilità di ottenere coppia) mentre altri si discostano ancora eccessivamente (probabilità di ottenere cinque carte diverse l'una dall'altra)

Dopo 200 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

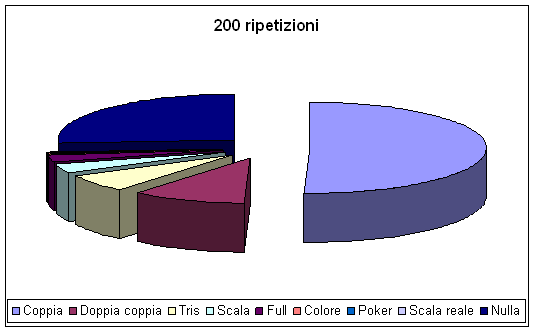
È facilmente riscontrabile come con l'aumentare delle prove eseguite i valori ottenuti siano a poco a poco sempre più simili a quelli calcolati matematicamente. Avessi avuto a disposizione tempo sufficiente a ripetere l'esperimento (2000\3000 volte) avrei, molto probabilmente, ottenuto percentuali ancora più simili a quelle ottenute a priori.

Quindi, per i fenomeni in cui è possibile calcolare la probabilità con la concezione classica (il gioco del poker è uno di questi) la frequenza, al crescere delle prove, tende generalmente ad avvicinarsi alla probabilità calcolata a priori.

A sostegno di questi dati, giungo ad enunciare la cosiddetta legge empirica del caso: in una serie di prove, ripetute un gran numero di volte, eseguite tutte nelle stesse condizioni, la frequenza tende ad assumere valori prossimi alla probabilità dell'evento e, generalmente, l'approssimazione è tanto maggiore quanto più numerose sono le prove eseguite.

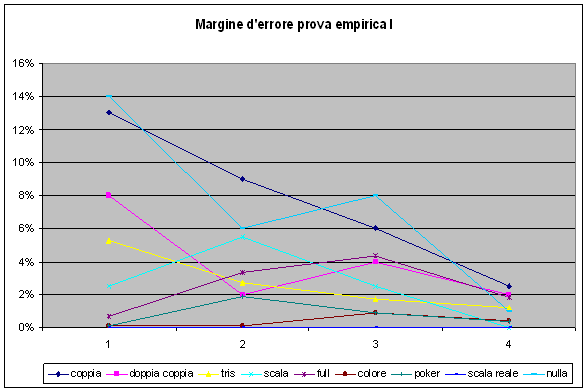
Nella prima tabella sono riassunti i risultati ottenuti, nella seconda il margine d'errore (il valore assoluto dell'errore, come si può vedere nella schermata di excel al fondo della relazione):

	Calcolata a priori	10 ripetizioni	50 ripetizioni	100 ripetizioni	200 ripetizioni
coppia
doppia coppia
tris
scala
full
colore
poker
scala reale
nulla

		10 ripetizioni	50 ripetizioni	100 ripetizioni	200 ripetizioni
coppia
doppia coppia
tris
scala
full
colore
poker
scala reale
nulla

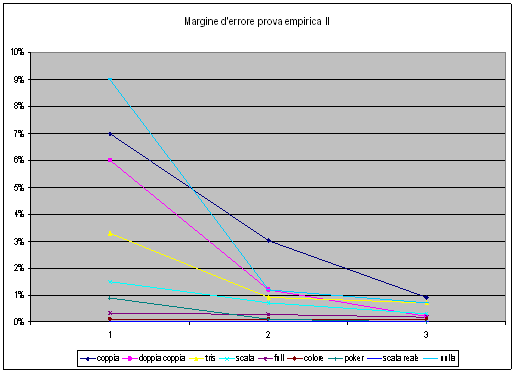
PROVA EMPIRICA n.2

mediante supporto informatico

Sfruttando un simulatore trovato su un sito internet ho ripetuto l'esperimento (estrarre 5 carte da un mazzo di 32) virtualmente.

Il vantaggio di questo metodo è che la prova può essere ripetuta migliaia di volte in tempi ragionevoli.

L'unico problema è che non posso avere l'assoluta certezza che il programma estragga le carte in modo casuale e non si basi invece su valori calcolati a priori.

Analizzando i risultati ottenuti sembrerebbe però che il programma estragga in modo casuale le serie di carte.

Andrò a questo punto ad illustrare i risultati ottenuti ripetendo la prova un numero di volte decisamente più elevato che nel caso precedente.

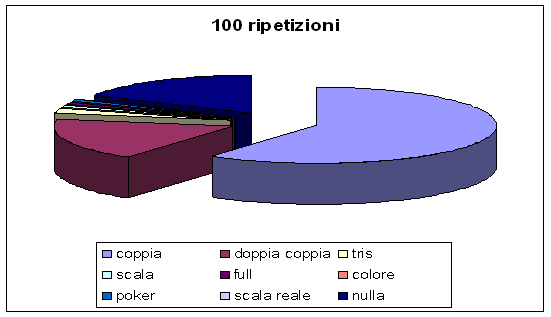
Dopo 100 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

Dopo 500 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

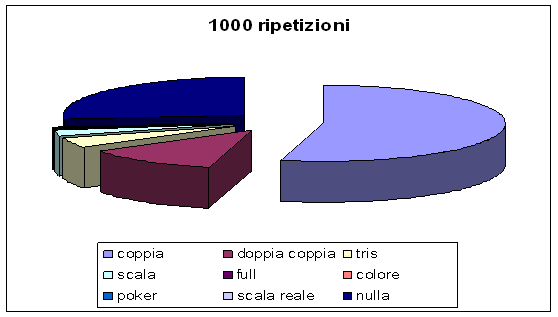
Dopo 1000 ripetizioni:

Punteggio	N. volte	Probabilità
Coppia
Doppia coppia
Tris
Scala
Full
Colore
Poker
Scala reale
Nulla

Come già fatto per la prima prova empirica, riporterò qui di seguito il riassunto dei risultati (nella prima) e la percentuale del margine d'errore (in valore assoluto) nella seconda:

	Calcolata a priori	100 ripetizioni	500 ripetizioni	1000 ripetizioni
coppia
doppia coppia
tris
scala
full
colore
poker
scala reale
nulla

		100 ripetizioni	500 ripetizioni	1000 ripetizioni
coppia
doppia coppia
tris
scala
full
colore
poker
scala reale
nulla