Se b è un numero reale, il prodotto bi si chiama numero immaginario.

Osserviamo che continua a valere la proprietà commutativa cioè         

bi=ib

I numeri bi e -bi si dicono numeri immaginari opposti o contrari.

L'addizione e la sottrazione di numeri immaginari dà come risultato un numero immaginario.

Il prodotto e il quoziente di due numeri immaginari sono numeri reali.

Siano a e b due numeri reali. Le espressioni della forma a+ib somma di un numero reale e di un numero immaginario prendono il nome di numeri complessi.

Il numero a si dice parte reale del numero complesso,ib è la parte immaginaria e b è il coefficiente dell'immaginario.

Se b=0,il numero complesso a+ib coincide con il numero reale a;

se a=0 il numero complesso coincide con il numero immaginario ib.

Due numeri complessi si dicono uguali quando hanno rispettivamente uguali le parti reali e i coefficienti dell'immaginario.

Due numeri complessi che hanno la stessa parte reale ed opposti i coefficienti dell'immaginario si dicono complessi coniugati.

Due numeri complessi si dicono opposti quando sono opposte sia la parte reale sia quella immaginaria.

La somma di due o più numeri complessi si definisce come il numero complesso che ha per parte reale la somma delle parti reali degli addendi e per coefficiente della parte immaginaria la somma dei coefficienti delle parti immaginarie:

(a+ib)+(c+id)=(a+c)+i(b+d).

Per differenza di due numeri complessi si intende la somma del primo e dell'opposto del secondo.

Si chiama reciproco del numero complesso c+id il numero:

moltiplicando numeratore e denominatore di questa frazione per il coniugato di c+id,cioè c-id,si ha:

==

Si può così affermare che il reciproco del numero complesso c+id è

Per quoziente di due numeri complessi si intende il prodotto del primo per il reciproco del secondo.

=

Rappresentazione geometrica dei numeri complessi

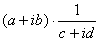
Così come i numeri reali si possono mettere in corrispondenza biunivoca con i punti di una retta, i numeri complessi si possono porre in corrispondenza biunivoca con i punti di un piano.

Fissiamo sul piano un sistema di assi cartesiani di origine O .

Il numero complesso è caratterizzato dalla coppia di numeri reali ; sia P il punto del piano di ascissa e di ordinata ,conveniamo di rappresentare il numero complesso con il punto P.Il punto P costituisce l'immagine geometrica del numero complesso dato,e viceversa,ad ogni punto del piano corrisponde un numero complesso avente per parte reale l'ascissa del punto P e per coefficiente della parte immaginaria l'ordinata del punto P.

In tal modo resta stabilita una corrispondenza biunivoca tra i punti P del piano e le coppie di numeri reali cioè tra i punti P del piano e i numeri complessi .

Se il numero complesso si riduce ad che è reale e il punto P viene a trovarsi sull'asse ,che si dice perciò asse reale.

Se si ha il numero immaginario e il punto P viene a trovarsi sull'asse .

L'origine O è l'immagine dello zero complesso .

Il piano considerato come luogo dei punti immagini geometriche dei numeri complessi si dice piano di Gauss .

Oss. Nel piano di Gauss,due numeri complessi coniugati hanno per rispettive immagini due punti simmetrici rispetto all'asse reale (asse ) e due numeri opposti invece sono rappresentati da punti

simmetrici rispetto all'origine O degli assi.

y

P

b

O a Q x

Corrispondenza tra vettori e numeri complessi

Abbiamo visto che al numero complesso possiamo associare il punto P del piano di Gauss di coordinate ,ma il punto P individua il vettore OP, quindi possiamo dire che al numero complesso corrisponde il vettore avente come sua componente secondo l'asse e come componente secondo l'asse .

Viceversa,in un piano ,ogni vettore può rappresentarsi con un numero complesso avente per parte reale e per coefficiente dell'immaginario le componenti del vettore rispettivamente secondo l'asse e l'asse .

Esiste quindi una corrispondenza biunivoca tra i numeri complessi e i vettori del piano.

Forma trigonometrica dei numeri complessi

Sia OP il vettore corrispondente al numero complesso e sia il modulodel vettore e l'angolo che il vettore forma con la direzione positiva dell'asse x. Dal triangolo rettangolo OQP si ha:

,

da cui

e (1)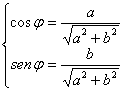

I due numeri e si dicono rispettivamente modulo ed argomento del numero complesso ; si suol dire che a+ib è la forma algebrica del numero complesso ,numero che si può mettere sotto la forma trigonometrica :

è positivo (ed è nullo solo se a=b=0), mentre l'argomento è determinato a meno di un multiplo intero di (o di 360°).

Se è un angolo notevole,il suo valore può essere immediatamente ricavato dalle (1); altrimenti, sempre dalle (1) e per si deduce e, con una calcolatrice si determina arctg.

Si ottiene così un angolo positivo del primo quadrante o un angolo

negativo del quarto quadrante .

Se a>0 ,ossia ,poiché è un angolo del primo o quarto quadrante ,si può assumere ;

Se a<0 ,ossia , è un angolo del secondo o terzo quadrante e si assumerà quindi ;

   

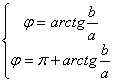
I numeri reali hanno per argomento 0 o a secondo che siano positivi o negativi ; invece i numeri immaginari hanno per argomento oppure ,secondo che il coefficiente di i sia positivo o negativo .

Prodotto di due numeri complessi sotto forma trigonometrica

Siano dati due numeri complessi

Eseguiamo il prodotto:

=

Possiamo quindi concludere che : il prodotto di due numeri complessi ha per modulo il prodotto dei moduli e come argomento la somma degli argomenti

Quoziente di due numeri complessi sotto forma trigonometrica

Procediamo analogamente per calcolare il quoziente:

Possiamo concludere che:il quoziente di due numeri complessi ha come modulo il quoziente dei moduli e come argomento la differenza degli argomenti

Potenza di un numero complesso

Consideriamo un numero complesso posto in forma trigonometrica:

vogliamo calcolare :

basterà applicare la regola del prodotto di due numeri complessi per avere:

=

che è la cosiddetta formula di Moivre .

Radici_ dei numeri complessi

Risolviamo ora il problema inverso del precedente:dato un numero complesso ,in forma trigonometrica,vogliamo trovare i numeri

che sono le radici di ,tali cioè che sia

dove n è un numero intero positivo .

Dimostreremo che,nel campo dei numeri complessi,l'estrazione di radice è un operazione sempre possibile ed inoltre ogni numero complesso ammette n radici diverse .

Dato il numero complesso

cerchiamo di determinare le sue radici ,che indicheremo

.

per definizione risulta

=

.

Perché questa eguaglianza sia soddisfatta deve essere:

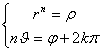
da cui

,

La radice n-esima di è ovviamente intesa in R ed ha quindi un unico valore positivo o nullo; per ottenere n radici diverse,possiamo assegnare a k ad esempio i valori 0,1,2,.,(n-1).

Concludendo si ha :

=

dove k assume i valori 0,1,2,.,(n-1).

Forma esponenziale dei numeri complessi

I numeri complessi si possono anche rappresentare in forma esponenziale .Se si pone per definizione

allora si ha, per un generico numero complesso

La (1) è detta formula di Eulero e definisce la potenza ad esponente immaginario del numero e=2,7182. (numero di Nepero).

Mostriamo che per le potenze ad esponente immaginario restano valide le proprietà formali delle potenze ad esponente reale.

1)Qualunque sia R ,è sempre diverso da zero.

Infatti se fosse =0 per qualche valore di dovrebbe essere,

per la (1), ,cioè ,il che è impossibile.

Infatti il secondo membro della (1) rappresenta un numero com-

plesso in forma trigonometrica di modulo unitario e quindi ri-

cordando come si esegue il prodotto di due numeri complessi in

forma trigonometrica si ha

infatti

E' evidente a questo punto come si possa operare con i numeri complessi dati in forma esponenziale.

Siano ;

allora si ha

Dato poi in numero complesso si ha pure

    ; con

Forma polare dei numeri complessi

Un punto del piano può essere identificato oltre che con le sue coordinate cartesiane anche con le sue coordinate polari, definendo come modulo del punto la sua distanza dall'origine ,

e come suo argomento l'angolo che esso forma con l'asse x.

y

P

b

O       a Q x

Abbiamo che : , quindi il punto P ha coordinate cartesiane (x;y) e coordinate polari ().

Un numero complesso viene individuato tramite le coordinate polari del punto P sua immagine nel piano di Gauss,e scriveremo:

Pertanto

e

sono le formule che ci permettono di passare dalla forma polare di un numero complesso a quella algebrica .

Viceversa per passare dalla forma algebrica a quella polare useremo le formule:

      e

La moltiplicazione e la divisione sono generalmente meno complicate quando si usa la forma polare.

In generale si ha:

= ;

        .