|
|
| |
2G. EQUISCOMPONIBILITA' NEL PIANO ED AREE
§1. La relazione di equiscomponibilità nel piano
Definizione. Chiameremo interni i punti di un poligono che non appartengono ai suoi lati, perimetrali i punti del poligono che appartengono ai suoi lati. I punti esterni ad un poligono sono invece tutti i punti dello spazio che non gli appartengono.
Dato un poligono P, i punti dello spazio S si ripartiscono quindi in 3 figure I, F ed E:
I=,
F= ed
E=.
Si ha:
P=I F; P E=
Valgono inoltre le equazioni:
I F E=S e
I F=I E=F E=
che definiscono la partizione dello spazio.
 Definizione. Chiameremo confinanti
due poligoni aventi in comune uno o più punti perimetrali, e solo perimetrali.
Definizione. Chiameremo confinanti
due poligoni aventi in comune uno o più punti perimetrali, e solo perimetrali.


Dati due poligoni confinanti, sono possibili solo due casi: o hanno in comune punti perimetrali "isolati", su qualche lato; o hanno qualche segmento in comune sui lati. In entrambi i casi abbiamo la
Definizione. Si chiama somma di due o più poligoni confinanti A, B, C... la figura A B C....
È facile vedere che la somma di poligoni confinanti è ancora un poligono: la figura A B C... è infatti una parte di piano compresa entro una poligonale ch 949b11j iusa. Poiché l'unione tra insiemi gode delle proprietà commutativa ed associativa, delle stesse gode la somma di poligoni confinanti. Viceversa, si ha la
Definizione. Dato un poligono P, esso si dice scomposto nei poligoni confinanti A, B, C,..., se A B C...=P; cioè se P è la somma dei poligoni confinanti A, B, C,...
Definizione fondamentale. Due poligoni A e B si dicono equiscomponibili se sono la somma di poligoni confinanti congruenti. Scriveremo A B.
Se chiamiamo P l'universo di tutti i poligoni, la definizione precedente stabilisce quindi una relazione interna E P² in P
E
La relazione E (detta equiscomponibilità) gode di 4 proprietà:
(senza nome). Se due poligoni sono congruenti, allora sono equiscomponibili: A B A B;
riflessiva. Ogni poligono è equiscomponibile a se stesso: A A;
simmetrica. Se un poligono è equiscomponibile ad un secondo, il secondo è equiscomponibile al primo: A B B A;
transitiva. Se un poligono è equiscomponibile ad un secondo ed il secondo è equiscomponibile ad un terzo, allora il primo è equiscomponibile al terzo: A B /\ B C A C.
Dimostrazione. La dimostrazione delle prime 3 proprietà è immediata; osserviamo soltanto che per la prima non vale l'inverso, cioè due poligoni possono essere equiscomponibili senza essere congruenti. La quarta proprietà richiede invece un ragionamento più elaborato:
I) scomponiamo A e B in poligoni congruenti (ciò è possibile perché A B);
II) scomponiamo ora B e C in poligoni congruenti (e ciò è possibile perché, per ipotesi, anche B e C sono equiscomponibili);
III) B è stato così scomposto in due maniere diverse: osserviamo ora la sua scomposizione "complessiva", cioè la scomposizione di B che si ottiene sovrapponendo le due scomposizioni;
IV) essa rappresenta una scomposizione comune per A e per C, che quindi risultano equiscomponibili. C.v.d.
E è quindi una relazione di equivalenza interna ad P. Allora possiamo costruire l'insieme quoziente
Q P E
che ha per elementi le classi di equivalenza [P] di P
[P]=,
Q
Definizione. Una classe di equivalenza [P] si chiama area.
L'area di un poligono P è quindi ciò che esso condivide con tutti i poligoni equiscomponibili con esso. E se due poligoni non sono equiscomponibili? si possono in qualche modo confrontare? La risposta è positiva, e data dal seguente teorema che non dimostreremo:
Teorema. Se due poligoni P e Q non sono equiscomponibili, sono possibili solo due casi: o P è equiscomponibile a un poligono Q' Q, o Q è equiscomponibile ad un poligono P' P; cioè
- o P Q' Q,
- o Q P' P.
Nel primo caso scriveremo P<Q, nel secondo P>Q, ed useremo gli aggettivi "minore" e "maggiore" per indicare le due relazioni, dato che esse - come si potrebbe dimostrare - godono delle proprietà delle relazioni d'ordine. Ricapitolando, due poligoni P e Q si possono sempre confrontare tra loro e i casi sono 3, uno escludente l'altro:
o sono equiscomponibili: P Q;
o il primo è minore del secondo: P<Q;
o il primo è maggiore del secondo: P>Q.
Ne discende il seguente importante
Corollario. L'insieme P dei poligoni è una classe di grandezze omogenee.
Dimostrazione. Basta prendere come relazione di equivalenza nella classe la relazione di equiscomponibilità , come relazioni d'ordine quelle di minoranza < e di maggioranza >, e come addizione di due poligoni P e Q l'unione di due poligoni confinanti P' e Q', rispettivamente tali che P P' e Q Q'. Gli assiomi di Eudosso e di Archimede vengono senz'altro assunti. È facile verificare che allora valgono tutte le relazioni e le operazioni (con le necessarie proprietà formali) per una classe di grandezze omogenee. In particolare, l'elemento nullo O è la classe di equiscomponibilità dei poligoni coincidenti con un segmento o un punto. C.v.d.
§2. Unità di misura delle aree
Poiché l'universo dei poligoni P costituisce una classe di grandezze omogenee, possiamo
a) confrontare due poligoni A e B tra loro, per vedere se A B (diremo allora che i due poligoni hanno la stessa area), oppure se A è minore di B (diremo che A ha area minore di B), oppure se A è maggiore di B (A ha area maggiore di B);
b) moltiplicare un poligono A per un numero reale non negativo a, ottendo un nuovo poligono B aA, anzi una classe di poligoni [B] tra loro tutti equiscomponibili. Diremo che l'area di B è a volte l'area di A.
Ha senso anche fare il rapporto di due poligoni:
A/B:
ciò che si ottiene è un numero reale a, quello che moltiplicato per B dà A:
A/B=a aB A.
 Infine ha senso l'operazione di
misura che, per i poligoni si chiama misura dell'area: basta preventivamente
scegliere un'unità di misura u, che
in questo caso deve essere un poligono. Noi sceglieremo come unità di misura u il quadrato di lato 1 m:
Infine ha senso l'operazione di
misura che, per i poligoni si chiama misura dell'area: basta preventivamente
scegliere un'unità di misura u, che
in questo caso deve essere un poligono. Noi sceglieremo come unità di misura u il quadrato di lato 1 m:
e lo chiameremo metro quadrato (m²). Dire dunque che l'area di un poligono misura 3 m² significa dire che il poligono è equiscomponibile ad un poligono 3u:


 Quello in figura è un possibile
poligono equiscomponibile di classe [3u];
ma ce ne sono evidentemente ; per es., un altro è
Quello in figura è un possibile
poligono equiscomponibile di classe [3u];
ma ce ne sono evidentemente ; per es., un altro è

un altro ancora

ecc. ecc. Tutti hanno area 3u=3m². L'importante risiede nel fatto che, scelta una volta per tutte come unità di misura il m², ogni poligono P è misurabile, cioè ogni poligono ha una determinata area data dal numero
a=P/u:
questo numero, come sappiamo, è un numero reale non negativo. Dunque
Definizione. Si chiama misura dell'area d'un poligono il numero reale non negativo che si ottiene facendo il rapporto tra il poligono e l'unità di misura u.
Dire che cos'è la misura dell'area non è evidentemente la stessa cosa che calcolarla: per qualche poligono dalla forma strana può infatti risultare difficile trovare la misura a. Degli algoritmi per calcolare a nel caso dei poligoni più comuni sono presentati nei prossimi paragrafi.
§3. Poligoni equiscomponibili
Teorema. Un parallelogramma è equiscomponibile al rettangolo avente uguale base ed uguale altezza.
Dimostrazione. Consideriamo una striscia di larghezza h, ed inseriamo al suo interno un parallelogramma di base b (EFCD) ed il rettangolo (che è unico avente base b ed altezza h) ABCD:
A E B F

h
![]()
D C
Dimostriamo che ABCD EFCD. Il rettangolo si può scomporre nel triangolo AED e nel trapezio DEBC:
ABCD AED+DEBC;
il parallelogramma è invece scomponibile nel trapezio DEBC e nel triangolo BFC:
EBCD BFC+DEBC.
Osserviamo ora che i due triangoli AED e BFC sono congruenti e quindi rettangolo e parallelogramma sono equiscomponibili perché somma di poligoni confinanti congruenti. C.v.d.
Ho scelto nella striscia un parallelogramma arbitrario: se ne avessi scelto un altro, con la stessa base b e la stessa altezza h, anch'esso sarebbe risultato equiscomponibile al rettangolo ABCD. Quindi, per la proprietà transitiva della relazione , tutti i parallelogrammi aventi la stessa base e la stessa altezza sono equiscomponibili tra loro. Abbiamo così ricavato il
Corollario. Tutti i parallelogrammi aventi base ed altezza rispettivamente congruenti sono equiscomponibili.
Teorema. Un rombo è equiscomponibile alla metà di un rettangolo avente per lati le diagonali del rombo.
Dimostrazione. Se tracciamo il rettangolo circoscritto al rombo e le diagonali di quest'ultimo, si vede subito che il rettangolo è composto di 8 triangoli rettangoli congruenti e che il rombo è composto di 4 di questi triangoli rettangoli. Quindi il rombo ½ rettangolo. C.v.d.

![]()
Teorema. Un triangolo è equiscomponibile alla metà di un parallelogramma avente la stessa base e la stessa altezza.
Dimostrazione. Sia ABC il triangolo, h l'altezza, BC la sua base; ACBD un parallelogramma avente la stessa base e la stessa
A D
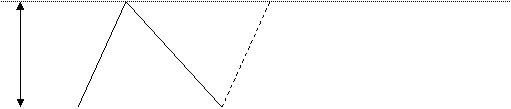
h
![]()
C B
altezza del triangolo. Per la prima proprietà dei parallelogrammi, i due triangoli ABC e ABD sono congruenti: quindi
ABC ½ACBD. C.v.d.
Corollario. Tutti i triangoli aventi la stessa base e la stessa altezza sono equiscomponibili tra loro.
Teorema. Un trapezio è equiscomponibile a un triangolo avente la stessa altezza e per base la somma delle basi del trapezio.
Dimostrazione. Consideriamo la figura, dove il trapezio ABCD
A B
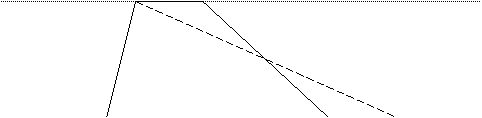
O
![]()
D C E
ha la base minore AB congruente al tratto CE della base DE del triangolo AED; inoltre i due poligoni hanno la stessa altezza, che è la larghezza della striscia. I due triangoli AOB e COE sono congruenti per il secondo criterio, poiché hanno i lati AB e CE congruenti per costruzione e gli angoli adiacenti ai lati uguali perché alterni interni di rette parallele tagliate da una trasversale. Quindi trapezio e triangolo sono equiscomponibili tra loro, in quanto somma di una parte comune (il quadrilatero AOCD) e di due triangoli congruenti. C.v.d.
Sappiamo che un poligono regolare (cioè equiangolo ed equilatero) ha sia la circonferenza incritta sia la circonferenza circoscritta, e che queste sono concentriche, avendo lo stesso centro che si chiama centro del poligono regolare. Sappiamo inoltre che il raggio della circonferenza inscritta si chiama apotema del poligono, mentre il raggio della circonferenza circoscritta si chiama raggio del poligono. Uniamo ora il centro del poligono con tutti i suoi vertici: otteniamo dei triangoli (tanti quanti sono i lati del poligono) aventi tutti la stessa altezza (l'apotema), ed aventi per basi i lati. Dunque
Teorema. Un poligono regolare è equiscomponibile ad un triangolo avente per lato il perimetro del poligono e per altezza l'apotema. Questo teorema vale, a pensarci bene, per tutti i poligoni circoscrittibili ad un cerchio.

§4. Teoremi di Euclide e Pitagora
I° Teorema di Euclide. In un triangolo rettangolo, il quadrato costruito su un cateto è equiscomponibile al rettangolo avente per lati l'ipotenusa e la proiezione del cateto sull'ipotenusa.
![]()
![]() F
F
G P
A


Q
 E
E

B H C
![]() R
R
 Dimostrazione. Dobbiamo dimostrare che Q R, dove l'altezza di R è congruente alla proiezione BH
del cateto AB sull'ipotenusa BC. Il parallelogramma P ha la stessa base e la stessa
altezza del quadrato Q,
quindi è equivalente a Q. D'altro canto i due triangoli rettangoli ABC e EFB sono
evidentemente congruenti: quindi hanno le ipotenuse congruenti: BF BC. Allora il parallelogramma P ed il rettangolo R sono equiscomponibili, perché
hanno la stessa base e la stessa altezza. Per la proprietà transitiva della
relazione di equiscomponibilità, infine, Q R. C.v.d.
Dimostrazione. Dobbiamo dimostrare che Q R, dove l'altezza di R è congruente alla proiezione BH
del cateto AB sull'ipotenusa BC. Il parallelogramma P ha la stessa base e la stessa
altezza del quadrato Q,
quindi è equivalente a Q. D'altro canto i due triangoli rettangoli ABC e EFB sono
evidentemente congruenti: quindi hanno le ipotenuse congruenti: BF BC. Allora il parallelogramma P ed il rettangolo R sono equiscomponibili, perché
hanno la stessa base e la stessa altezza. Per la proprietà transitiva della
relazione di equiscomponibilità, infine, Q R. C.v.d.
Corollario (detto Teorema di Pitagora). In un triangolo rettangolo la somma dei quadrati costruiti sui cateti S equiscomponibile al quadrato costruito sull'ipotenusa.

Q'
![]()

 Q"
Q"
Q
R" R'
![]()
Dimostrazione. Per il primo teorema di Euclide Q' R' e Q" R": allora, sommando membro a membro, Q'+Q" R'+R" Q. C.v.d.
II° Teorema di Euclide. In un triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa è equiscomponibile al rettangolo avente per lati le proiezioni dei cateti sull'ipotenusa.
A
![]()
![]()
![]()

 Q
Q

Q'
![]()
![]()
![]()
![]() B H C
B H C
Q" R'
R
![]()
Dimostrazione. Dobbiamo dimostrare che Q' R'. Per il primo teorema di Euclide, applicato al triangolo rettangolo ABC, si ha: Q R=Q"+R'. Per il teorema di Pitagora, applicato al triangolo rettangolo ABH, si ha: Q Q'+Q". Dunque, per la proprietà transitiva: R Q'+Q", ossia Q"+R' Q'+Q" e quindi Q' R'. C.v.d.
§5. Misura dell'area dei poligoni
Abbiamo scelto come unità di misura u delle aree il m², cioè il quadrato di lato 1 m. Misurare l'area d'un poligono significa trovare quel numero reale non negativo a che dice quante volte il poligono dato contiene u: questa è un'operazione generalmente difficile, perché quasi mai il quadrato u m² si adatta perfettamente ai contorni del poligono, e dovremmo perciò riuscire a trovare una scomposizione comune all'uno e all'altro. Misurare invece la lunghezza d'un segmento è un'operazione molto più facile, perché non esiste alcun problema a vedere quante volte l'unità di misura (che in questo caso è il metro = 1m) ed i suoi sottomultipli (dm, cm, mm,...) sono contenuti nel segmento da misurare. (Naturalmente se il segmento è molto lungo, e per di più, con un estremo inaccessibile, come la distanza Terra-Luna, la misurazione può essere laboriosa; così come laboriosa è la misurazione d'un segmento molto corto come il raggio dell'atomo di H). In ogni caso la misura d'un segmento è più facile di quella di un'area. Vogliamo allora vedere se è possibile trovare la misura dell'area di un poligono a partire dalle misure della lunghezza di alcuni segmenti che lo caratterizzano (lati, diagonali, altezze).
Teorema. La misura dell'area del rettangolo è uguale al prodotto della misura della base per la misura dell'altezza.
Dimostrazione. Prima di eseguire la dimostrazione, facciamo un'osservazione: si è soliti dire che l'area di un rettangolo è base per altezza. Ora questa è una maniera molto imprecisa di parlare. Infatti la base è un segmento, l'altezza anche, e come si può "moltiplicare" un segmento per un altro? Questa operazione non esiste. Noi possiamo moltiplicare un segmento per un numero reale non negativo (ed otteniamo così un altro segmento), ma non esiste in Matematica l'operazione di moltiplicazione di due segmenti. Tantomeno poi, possiamo dire che il risultato di un'operazione così fantomatica possa produrre un'area, che è un elemento dell'insieme quoziente Q P E ! La maniera corretta di esprimersi è un'altra: la misura dell'area (che è un numero reale non negativo) è il prodotto delle misure (che sono altri due numeri reali non negativi) della base e dell'altezza. Ora sì ha senso di parlare di prodotto: la moltiplicazione avviene infatti tra numeri reali, ed il risultato è un altro numero reale. Passiamo ora alla dimostrazione. Dividendo base ed altezza del rettangolo per 1m, si ottiene la misura b della base (b R ) e la misura h dell'altezza (h R ), ed allo stesso tempo il rettangolo viene diviso in tanti quadrati u=1m² quanti sono dati dal numero a=bh. C.v.d.

h=12 m area=12x24 m²
b=24 m
Corollario 1. La misura dell'area del quadrato il cui lato misura l m è l ² m².
Tutte conseguenze del teorema principale e dei teoremi del paragrafo precedente sull'equiscomponibilità dei poligoni sono i seguenti corollari:
Corollario 2. La misura dell'area d'un parallelogramma è il prodotto delle misure della base e dell'altezza.
Corollario 3. La misura dell'area d'un triangolo è il semiprodotto della misura della base per la misura dell'altezza.
Corollario 4. La misura dell'area del rombo è il semiprodotto delle misure delle sue diagonali.
Corollario 5. La misura dell'area del trapezio S il semiprodotto della somma delle misure delle basi per la misura dell'altezza.
Corollario 6. La misura dell'area d'un poligono circoscrittibile ad una circonferenza è il semiprodotto della misura del perimetro per la misura dell'apotema.
Ricapitoliamo le formule
|
Poligono |
Area |
|
Rettangolo |
bh |
|
Parallelogramma |
bh |
|
Quadrato |
l² |
|
Triangolo |
½ bh |
|
Rombo |
½ Dd |
|
Trapezio |
½ (B+b)h |
|
Poligono circoscrittibile |
½ Pa |
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024