|
|
| |
Vettori (sintesi e
introduzione)
I vettori sono gli oggetti matematici che costituiscono la base di tutte le
teorie fisiche.
Esponiamo qui i concetti fondamentali della teoria dei vettori limitatamente al
caso dei vettori dello
spazio (tridimensionale) della nostra esperienza (ed in
particolare del piano (bidimensionale))
tenendo presente che tali concetti possono essere estesi a spazi a più
dimensioni ed addirittura a
spazi astratti formati oggetti astratti quali le funzioni.
Tali estensioni vengono approfondite in altre pagine di questo sito.
Un vettore si può rappresentare come un segmento dotato di una freccia.
Un generico vettore V dello spazio ha 3 componenti
rispetto ad un sistema di coordinate
cartesiane ortogonali ed è indicato come ![]() .
.
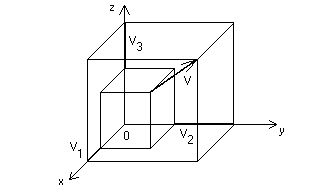
Seguendo l'usuale formalismo degli indici, possiamo inoltre indicare il
vettore V tramite le sue
componenti, ovvero useremo indipendentemente V e ![]() per esprimere il vettore stesso (l'indice
per esprimere il vettore stesso (l'indice
i assume i valori interi 1, 2 , 3 ).
Ribadiamo ulteriormente il significato di componente di un vettore rispetto ad
un sistema di coordinate
cartesiane tramite il seguente esempio nel piano :
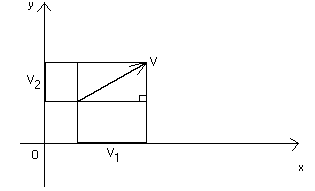
dove il vettore V può essere "applicato" in qualunque
punto.
Un vettore possiede un modulo o intensità (o norma ) che ne
rappresenta la lunghezza definibile
tramite il teorema di Pitagora. Il modulo del vettore V è
indicato con |V| e vale :
![]() nello spazio 424d31e
nello spazio 424d31e
e :
![]() nel piano.
nel piano.
01 - Operazioni elementari.
Esiste il vettore nullo le cui componenti sono tutte nulle e che ha
perciò modulo 0 . Esso coincide
con l'origine 0 del sistema di assi cartesiani. Esso è :
0 = (0 , 0 , 0)
e per ogni vettore V esiste il vettore inverso
-V ottenuto moltiplicando per -1 tutte le sue
componenti per cui :
![]() .
.
Il vettore inverso di un vettore dato è quel vettore di uguale direzione,
intensità ma di verso opposto.
Dati i due vettori A e B , si definisce per addizione
l'operazione che fa ottenere come risultato il
vettore C = A + B le cui componenti sono date dalla somma
delle corrispondenti componenti :
![]() dove i = 1, 2, 3 .
dove i = 1, 2, 3 .
L'addizione fra due vettori ha una importante interpretazione grafica che va
sotto il nome di regola
del parallelogramma. Nel piano :
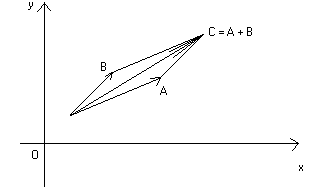
Questa regola corrisponde in fisica alla legge di composizione delle forze.
Dati uno scalare (numero reale) k ed un vettore A , si
definisce la moltiplicazione per uno scalare
come l'operazione che fa ottenere per risultato il vettore B = k A
le cui componenti sono date dal
prodotto di k per le corrispondenti componenti di A :
![]() dove i = 1, 2, 3 .
dove i = 1, 2, 3 .
Moltiplicando un vettore per k si ottiene un altro vettore di
uguale direzione, intensità moltiplicata
per |k| e stesso verso, se k è positivo, o verso
opposto, se k è negativo.
Ovviamente, moltiplicando un vettore per -1 si ottiene il vettore
inverso e moltiplicando un vettore
per 0 si ottiene il vettore nullo.
02 - Prodotto scalare.
Fra due vettori A e B è possibile definire due tipi di
moltiplicazione : quella scalare, che dà come
risultato uno scalare, e quella vettoriale, che dà come risultato un vettore.
Di queste presentiamo qui la prima, il cosiddetto prodotto scalare.
Il prodotto scalare (o prodotto interno) fra due vettori è definito come
la somma dei prodotti delle
componenti corrispondenti ed è indicato con il simbolo · ,
ovvero :
![]() .
.
Sottolineiamo il fatto che il risultato ![]() del
prodotto scalare è uno scalare (cioè un numero).
del
prodotto scalare è uno scalare (cioè un numero).
Il prodotto scalare assume l'importante significato geometrico di essere uguale
al prodotto del modulo
del primo vettore per la proiezione dell'altro vettore sulla direzione su cui
giace il primo.
Graficamente, nel piano :
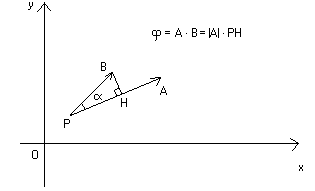
Una tipica applicazione fisica del prodotto scalare è il lavoro. Quando
una forza subisce uno
spostamento vi è lavoro ed il suo valore è appunto dato dal prodotto scalare
fra il vettore
forza per il vettore spostamento.
Vettori (approfondimento)
![]() Il
cambiamento di posizione che corrisponde al passaggio da un punto A a un punto
B può essere descritto indicando la variazione orizzontale xB-xA, che indicheremo
anche con Δx, e la variazione verticale yB-yA, che indicheremo
anche Δy.
Il
cambiamento di posizione che corrisponde al passaggio da un punto A a un punto
B può essere descritto indicando la variazione orizzontale xB-xA, che indicheremo
anche con Δx, e la variazione verticale yB-yA, che indicheremo
anche Δy.
[Δx sta
per "d ifferenza delle x"; infatti Δ è la lettera
greca "delta" maiuscola, che si legge come la lettera italiana D]
|
Nel caso a
sinistra della figura a lato abbiamo Δx>0 e Δy>0: spostandosi
da A a B aumentano sia la ascissa che l'ordinata. |
|
La funzione (x, y) ![]() (x+Δx, y+Δy) viene chiamata traslazione di passi
Δx e Δy o traslazione determinata dal vettore
(Δx,Δy) o traslazione di vettore (Δx,Δy). Viene
indicata con TΔx, Δy o con Tv se v indica il vettore (Δx,Δy).
(x+Δx, y+Δy) viene chiamata traslazione di passi
Δx e Δy o traslazione determinata dal vettore
(Δx,Δy) o traslazione di vettore (Δx,Δy). Viene
indicata con TΔx, Δy o con Tv se v indica il vettore (Δx,Δy).
|
Dati due punti A e B, il
vettore AB viene indicato in uno dei due modi seguenti (nel primo la
"freccia" ricorda che si tratta della traslazione che porta A in B,
nel secondo il "meno" indica che è una specie di |
||||||
|
|
I vettori raffigurati a fianco sono uguali: sono diversi modi per indicare la traslazione di passi 8,4. |
|
||||||||||||
|
B-A =
(xB-xA, yB-yA) = (8,4) |
[La parola vettore nel linguaggio comune significa "portatore" (ad es. chi effettua la consegna di una merce viene chiamato "il vettore", il razzo impiegato per mettere in orbita un satellite artificiale viene chiamato "razzo vettore", .); deriva dal verbo latino vehere, che significa "portare" (dallo stesso verbo derivano: vettura, veicolo, .). È evidente il motivo per cui è stato scelto questo nome per i passi delle traslazioni]
|
|
|
|
Si definisce addizione tra vettori
la funzione che a due vettori v = (h , k ) e v = (h ,k ) associa il
vettore (h +h , k +k ), che viene indicato v + v e chiamato somma
di v e v . |
|
|
|
|
|
Il vettore w che occorre addizionare a v
per ottenere u è il vettore differenza u-v. Ha
come componenti la differenza delle componenti di v e u. Nel
caso a fianco: |
|
|
|
Per l'addizione tra vettori vale la proprietà
del riordino [
|
Noi abbiamo introdotto i vettori per descrivere i cambiamenti di posizione e la somma di vettori per descrivere l'effetto complessivo di due successivi cambiamenti di posizione. In fisica, la somma di vettori viene impiegata anche per rappresentare lo spostamento complessivo di un oggetto il cui movimento può essere visto come l'effetto di due diversi movimenti contemporanei: si fa la somma dei vettori che rappresentano gli spostamenti a cui darebbero luogo i due singoli movimenti.
Oltre agli spostamenti in fisica vengono
rappresentati con vettori anche le velocità, le forze e varie
altre grandezze:
. Si tratta di grandezze di cui si può dare una
descrizione completa indicando, oltre alla loro misura (intensità), la
loro direzione.
Ad esempio una forza di
dato un vettore v = (h, k), si chiama modulo
di v la distanza dalla posizione iniziale alla posizione finale dopo
l'applicazione della traslazione Tv, cioè (nell'ambito della
geometria ![]() euclidea):
euclidea):
![]() (Δx) + (Δy)
=
(Δx) + (Δy)
= ![]() h + k
h + k
. Si può, inoltre, dimostrare che la composizione
di due di queste grandezze [la composizione di due velocità, la composizione di
due forze, .] dà luogo alla grandezza [una velocità, una forza, .]
rappresentata dal vettore che è la somma dei vettori che rappresentano le due
grandezze di partenza.
Grandezze di questo genere (rappresentabili e componibili come
vettori) vengono dette grandezze vettoriali.
![]() Nota
Nota
In alcune situazioni (come quando un vettore è usato
per indicare la forza esercitata per far ruotare qualcosa, in cui ![]() l'effetto dipende anche
dalla distanza dal centro di rotazione) è importante considerare anche il punto
di applicazione, ossia distingure i vettori AB e CD che abbiano stesso modulo e
stessa direzione ma A e C non coincidenti. In questi casi si dice che AB e CD
sono diversi come vettori applicati: un vettore applicato è
interpretabile matematicamente come una coppia (A,v), dove A è il punto
a cui è applicato il vettore v; in pratica è un "segmento
orientato".
l'effetto dipende anche
dalla distanza dal centro di rotazione) è importante considerare anche il punto
di applicazione, ossia distingure i vettori AB e CD che abbiano stesso modulo e
stessa direzione ma A e C non coincidenti. In questi casi si dice che AB e CD
sono diversi come vettori applicati: un vettore applicato è
interpretabile matematicamente come una coppia (A,v), dove A è il punto
a cui è applicato il vettore v; in pratica è un "segmento
orientato".
In un contesto in cui si stiano considerando vettori applicati, a
volte si usa la dizione "vettore libero" invece che
"vettore" per specificare che non ci interessa il punto di
applicazione.
Nota 2 Qui abbiamo usato il concetto di direzione in modo intuitivo.
Alla voce ![]() direzioni e
funzioni circolari ne è data una definizione puramente matematica.
direzioni e
funzioni circolari ne è data una definizione puramente matematica.
Nota 3 Le grandezze fisiche che sono completamente individuate da un solo
valore numerico vengono dette scalari (basta una
"scala" numerica, senza indicazioni di direzione). Sono tali ad
esempio il tempo, la temperatura e la massa.
Il peso invece è una grandezza vettoriale: è una forza diretta
verso il centro di gravità; le masse si misurano in chilogrammi, le intensità
dei pesi e, più in generale, delle forze (oltre che in newton, unità di
misura usata dai fisici - 1 N è la forza esercitata da un corpo con massa di
Quando si considerano grandezze vettoriali che operano
lungo una retta fissata in genere si usa rappresentarle solo con dei numeri,
come se fossero grandezze scalari, e si danno loro segni opposti se hanno
direzioni opposte; ad esempio se indichiamo con
![]() Per
applicare il concetto di vettore a situazioni in cui intervengono grandezze
fisiche che non operano lungo un piano occorre estendersi al caso tridimensionale.
I punti nello
Per
applicare il concetto di vettore a situazioni in cui intervengono grandezze
fisiche che non operano lungo un piano occorre estendersi al caso tridimensionale.
I punti nello ![]() spazio a 3 dimensioni sono
rappresentati da terne di numeri reali; lo stesso accade per i vettori. Ad es.,
facendo riferimento alla figura sotto a sinsitra, il vettore AB è (Δx,
Δy, Δz) = (-1, 2, 3): per andare da A in B si sale di 3 (Δz =
3), si avanza nella direzione dell'asse y di 2 (Δy = 2) e si retrocede di
1 nella direzione dell'asse x (Δx = -1).
spazio a 3 dimensioni sono
rappresentati da terne di numeri reali; lo stesso accade per i vettori. Ad es.,
facendo riferimento alla figura sotto a sinsitra, il vettore AB è (Δx,
Δy, Δz) = (-1, 2, 3): per andare da A in B si sale di 3 (Δz =
3), si avanza nella direzione dell'asse y di 2 (Δy = 2) e si retrocede di
1 nella direzione dell'asse x (Δx = -1).
Il modulo viene definito riconducendosi alla distanza euclidea,
che nel caso tridimensionale è definita [![]() ] estendendo in modo
naturale quella del caso bidimensionale:
] estendendo in modo
naturale quella del caso bidimensionale:
![]() (Δx) + (Δy) + (Δz)
(Δx) + (Δy) + (Δz)
Nel caso
della figura d(A,B) = ![]() 14
= 3.74., e questo è anche il modulo del vettore AB.
14
= 3.74., e questo è anche il modulo del vettore AB.
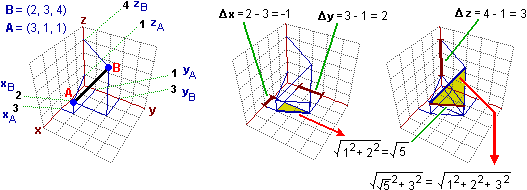
Sopra a destra viene motivata questa estensione: il segmento AB viene pensato nel piano verticale che lo contiene; la sua lunghezza è la radice quadrata della somma dei quadrati della variazione verticale, che è 4, e della variazione orizzontale, che viene ricavata come illustrato nella figura al centro, come distanza delle "proiezioni" di A e B sul piano individuato dagli assi x e y.
Esercizio1: testo e soluzione. Esercizio2: testo e soluzione
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024