TEOREMA DEL MOMENTO ANGOLARE

fisica

TEOREMA DEL MOMENTO ANGOLARE

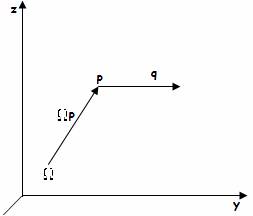
Consideriamo un punto materiale "P" che si muova in un sistema di riferimento inerziale. Sia q=m·v la sua quantità di moto, scegliamo un punto "Ω" di riferimento. Si chiama momento angolare o momento della quantità d 939h79j i moto del punto "P" rispetto al polo "Ω" il vettore:

p = ΩP × q

Partendo dal secondo principio della dinamica stabilirò l'equazione dinamica che governa l'evoluzione di "p":

f =

Moltiplicando ambo i membri per il vettore  "ΩP", si ha:

P × f = ΩP ×

Il primo membro di questa equazione è detto "momento della forza "f" rispetto al polo "Ω" e lo indichiamo con il simbolo "m":

m = ΩP × f

Ora possiamo scrivere il termine "m" nel modo seguente:

P × f = ΩP × m = P ×

Derivando: p = ΩP × q rispetto al tempo "t" avremo:

= ( P × q × q + ΩP ×

da cui

P × × q

Sostituendo si ha:

m = × q

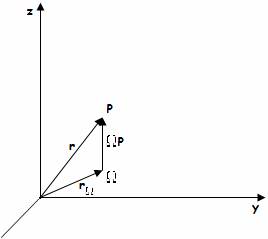
Osserviamo che il vettore "ΩP" può essere scritto come differenza fra il vettore posizione "r" del punto "P" e il vettore posizione "r " del punto Ω·ΩP = r-r da cui derivando e sostituendo si ha:

m = - (v v ) × q

Il vettore "v" ed il vettore "q" sono paralleli per cui il loro prodotto vettoriale è nullo,di conseguenza:

m = - (v v ) × q  m = v × q

dove:

v è la velocità del polo nel sistema di riferimento inerziale considerato

Se il polo è un punto fermo nel sistema di riferimento preso in esame si ha:

v m =

"Teorema del momento angolare"

In ogni sistema di riferimento inerziale, se si sceglie un punto fisso come polo, il momento risultante delle forze agenti su un punto materiale è pari alla derivata rispetto al tempo del momento angolare del puto materiale stesso.