|
|
| |
Lo sviluppo in serie di Fourier è un metodo per trattare le funzioni periodiche non sinusoidali.
Le forme d'onda dei segnali audio e televisivi, e di molte applicazioni, infatti, non sono mai sinusoidali, per cui è necessario descriverle matematicamente ricorrendo a metodi diversi da quelli usati per le sinusoidi o altre forme d'onda regolari.
Si considera una generica funzione periodica, f(t), con periodo pari a T. Essa può essere rappresentata dalla seguente equazione:
f(t)=f(t+mT) m=0,1,2,3,4,.
E' possibile studiare ed ottenere le funzioni matematiche di segnali periodici, considerando impulsi con lo stesso andamento (ossia, con un andamento altrettanto periodico).
Si ricorre, pertanto, al teorema di Fourier. Esso afferma che:
Una funzione periodica può essere espressa attraverso lo sviluppo in serie di Fourier. I seguenti passaggi si riferiscono ad uno sviluppo di soli seni.
f(T)=A0+F1sen(ωt+ )+F2sen(2ωt+ )+.+Fnsen(nωt+ n
![]()
![]()
f(T)=A0+∑Fnsen(nωt+ n
n=1
A0 rappresenta la componente continua ( o valore medio) ed ha ordine zero.
Essa è calcolabile eseguendo il rapporti tra l'area del periodo ed il periodo stesso:
A0=(aree positive - aree negative)/T

Ad essa è sommato un infinito numero di sinusoidi. La prima di esse è detta fondamentale, poiché la sua frequenza (f1=ω/2π) coincide con quella della funzione f(T).
Le altre armoniche hanno frequenza multipla di quella fondamentale ed ampiezza decrescente. Sono dette seconda, terza, quarta armonica, oppure armoniche di ordine due, tre, quattro e così via.
Il calcolo dell'ampiezza e della fase della fondamentale e delle armoniche è più complesso di quello della componente continua. E' generalmente effettuato per mezzo di programmi o consultazione di tabelle, in cui sono indicate le composizioni armoniche delle funzioni periodiche più comuni.
Inoltre risulta utile scomporre le armoniche in due componenti, una con fase 0 zero e l'altra 90°. Le due componenti sono dette sviluppo in seno e sviluppo in coseno ed hanno ampiezza:
An=Fnsenφn
Bn=Fncosφn
Riassumendo, si può esprimere una funzione periodica attraverso una serie di funzioni trigonometriche, attraverso lo sviluppo in serie di Fourier:
![]()
f(t)=A0+∑(Fnsennωt+Fncosnωt)
n=1
Il numero delle armoniche è illimitato ma, generalmente, la loro ampiezza decresce tanto rapidamente all'aumentare dell'ordine, da poter limitare il numero delle armoniche da considerare. Ovviamente, la scelta dell'ordine massimo dipende dalla precisione richiesta. Una approssimazione ottimale si ottiene considerando fino all'ordine undici.
E' inoltre importante considerare le condizioni di esistenza dello sviluppo di Fourier. Oltre alla periodicità, ci sono altre tre condizioni che devono verificarsi. Esse sono dette condizioni di Dirichlet:
Se la funzione f(t) presenta delle discontinuità, esse devono essere presenti in ogni periodo ugualmente;
La funzione f(t) deve avere un numero finito di massimi e minimi in un periodo, ossia un valore picco-picco limitato;
La funzione deve essere divisibile in periodi, per cui, se essa è aperiodica, è considerato con periodo un tempo infinito (T=∞).
RAPPRESENTAZIONE SPETTRALE DI AMPIEZZA E FASE
Per rappresentare la composizione armonica di un segnale, si ricorre allo spettro del segnale. Si rappresentano le armoniche di un segnale periodico nel piano cartesiano, in funzione della frequenza. Si possono considerare le armoniche in base alla loro ampiezza (spettro di ampiezza) o in base alla loro fase(spettrpo di fase).
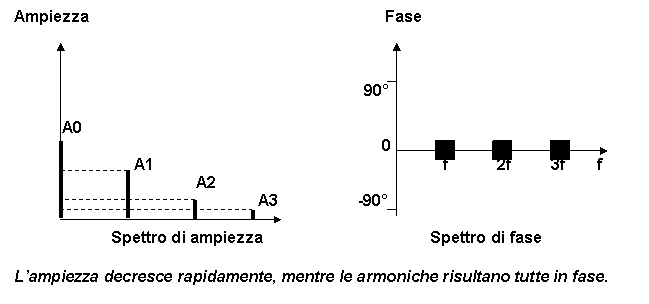
Tali rappresentazioni sono molto usate, in quanto permettono di descrivere le componenti elementari di ogni segnale (le righe spettrali).
Per visualizzare uno spettro si usa uno strumento detto analizzatore di spettro.
Esso è molto simile ad un oscilloscopio, ma si differenzia da quest'ultimo poiché, invece di considerare l'andamento delle ampiezze in funzione del tempo, lo considera in funzione della frequenza.
Inoltre, poiché non considera la fase di un segnale, le ampiezze negative e quelle positive sono rappresentate sullo stesso piano (quelle negative sono traslate di 180°).
TRASFORMATA DI FOURIER
Se si considera un segnale periodico, il suo periodo è un tempo finito. Se , invece il segnale è aperiodico, il suo periodo può essere inteso pari all'infinito (T=∞).
Poiché si considera il periodo tendente all'infinito (T ∞), la frequenza (f=1/T) tende ad essere pari a zero. Inoltre lo spettro delle armoniche del segnale risulta essere composto da righe più vicine, mentre, se la frequenza è elevata, esse tendono ad essere distanti fra loro.
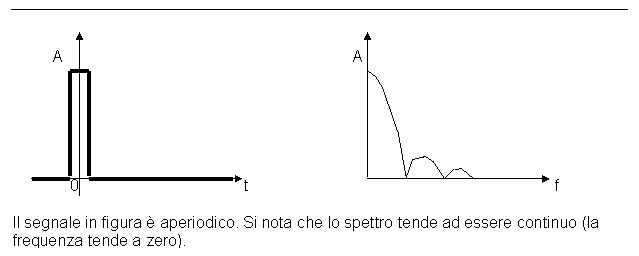
Partendo da una funzione descritta nel dominio del tempo, si può quindi ricavare la sua trasformata, ossia la stessa funzione descritta nel dominio delle frequenze. Essa riproduce ancora la funzione, ma in forma più comoda per i calcoli e la risoluzione dei problemi.
Utilizzando formule trigonometriche (le formule di Eulero) applicate alla serie di Fourier, si ottengono formule per ricavare la frequenza (le quali presentano integrali - Integrale di Fourier). Ricordando che le funzioni aperiodiche hanno uno spettro d'ampiezza che tende ad essere continuo, si può comprendere che, con l'integrale di Fourier (che è una funzione della pulsazione ω), possiamo descrivere una funzione aperiodica con una funzione continua sia in ampiezza che in fase.
Le armoniche dello sviluppo in serie si avvicinano sempre più, diminuendo in ampiezza e aumentando in frequenza. Le righe spettrali tendono così ad essere vicine quanto più la frequenza tende a zero.
La trasformata di Fourier è quindi l'insieme dei coefficienti che definiscono il campo delle frequenze del segnale periodico (o aperiodico). Si ottiene così uno spettro bilatero, di ampiezza e fase.
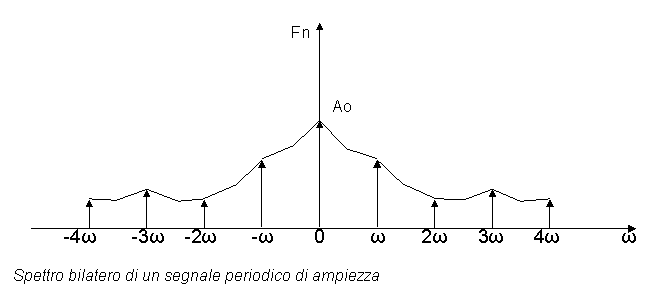
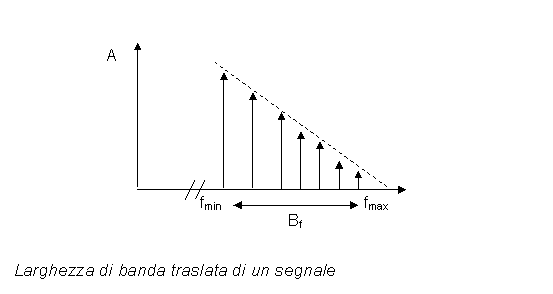
Bf=fmax-fmin
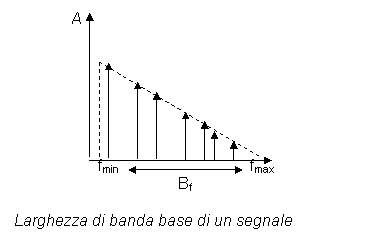
In base ad essa i segnali (periodici e aperiodici) si dividono in segnali in banda base e in banda traslata.
I segnali in banda base sono i segnali che hanno frequenza massima relativamente bassa (dell'ordine di decine di KHz al massimo). Essa deve rispettare la seguente condizione; deve essere almeno dieci volte maggiore della frequenza minima (fmax>10fmin).
![]()
I segnali in banda traslata sono quelli che hanno frequenza massima superiore alle decine di Khz (dell'ordine di centinaia di KHz). Si tratta di segnali che in genere hanno subito particolari trattamenti.
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024