Fluidodinamica

sistema propulsivo a pompa (cuore) suddiviso in 4 compartimenti

sistema di condotti messi in parallelo dove avviene lo scambio chimico/fisico

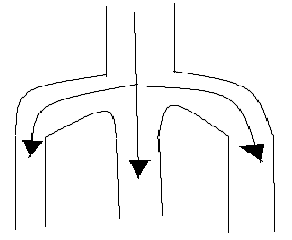
Sfruttando questa analogia squisitamente meccanica possiamo studiare le leggi che regolano i fluidi (fluidodinamica) ed applicarli al sistema circolatorio prima ed a interi organismi in seguito

Fluidodinamica

Dobbiamo partire da un sistema ideale, ossia in assenza di attriti e interventi di forze esterne al sistema.

Naturalmente terremo come base le leggi della conservazione della massa e dell'energia per estrapolare le nostre leggi.

Ovviamente un fluido è un sistema complesso, quindi nn potremo più trattare particelle singole, bensì sistemi formati da più particelle.

Definiamo perciò come unità base una PARTICELLA DI FLUIDO, con volume molto piccolo (10^-9) ma formata da un determinato numero di molecol 747b13h e; si tratta ovviamente in entrambi i casi di un volume medio.

A questo punto il nostro studio può avvenire a due livelli:

seguendo le particelle singole(spostamento, reazioni,.....)

seguendo il in comportamento delle particelle in un punto definito del fluido, metodo ovviamente privilegiato in quanto più facile da mettere in pratica

Nel caso da noi studiato sarà necessario conoscere la portata del liquido nel condotto e la sua eventuale variazione. Per farlo,conoscendo i seguenti dati

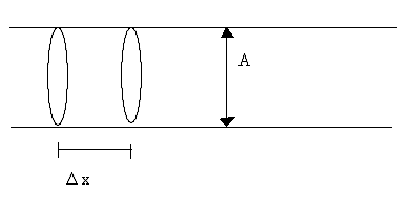A=sezione del condotto

ΔV=volume passante per la sezione

Δx=spazio percorso dal volume preso in considerazione

Definiremo la portata Q come

Q=ΔV/Δt in m³/s

Ossia il volume passante in un punto del condotto in un determinato periodo di tempo.

Tenendo conto delle seguenti equivalenze possiamo escogitare nuove equazioni per definire la portata

se ΔV=A*Δx ^_____ Q=A*(Δx/Δt) ^{______________}→ Q=A*v

v ovviamente intesa come velocità media delle particelle

La legge della conservazione della massa impone che, durante tutto il corso del condotto

Q=cost  e quindi A*v=cost

Cosa accade se A nn è costante ma varia nel corso del tubo?

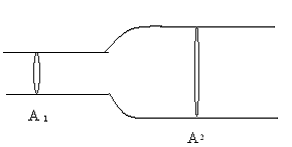
Considerando che Q è sempre costante, a variare saranno i parametri A e v.

Più di preciso

se   A₁<A₂ → v₁>v₂

A₁>A₂ → v₁<v₂

Applicando questi termini al sistema circolatorio

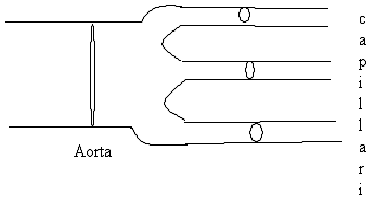
L'equazione di continuità continua a funzionare, in quanto la divisione dell'aorta in tanti capillari può essere vista come la divisione in un solo condotto con A uguale alla somma di tutte le A dei singoli capillari

es

v= 0.33 m/s Q=? l/min

r=9mm

A= r²    → Q= r²v

0,0025m²*0,33m/s = 8,4*10^-5 m³/s = 5l/min

es 2

d_i= 2cm

fori N:24 d=0,12cm

v_tubo= 1m/s

v_cap

H_{max spruzzo verticale}

Q= 3,14cm²*100cm/s = 314cm³/s

v= 314cm³/s / 24 = 13,5 /0,0113cm² = 1194m/s = 11,94m/s

oppure, impostandol'equivalenza

π*r²v₁ = 24 (πr²)*v_e

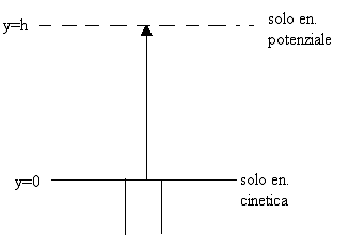
imposto, grazie alla legge di conservazione dell'energia, l'equazione

en. cinetica= energia potenziale

mgh = 1/2mv_e²

h = 6,8m

Lavoro nei fluidi

Ovviamente dobbiamo tenere conto de lavoro necessario a muovere l fluido lungo il tubo, grazie all'equazione

L = ΔK + ΔU

cinetica potenziale

Dobbiamo anche tenere conto della pressione, data dalla forza imposta s una data superficie di fluido

P = F/A in N/m²=Pa

unità di pressione: 1atm = 102.325Pa

1mmHg = 133.3 Pa

1bar = 100KPa= 100000Pa

in base alle affermazioni sopra riprodotte possiamo vedere

L = P*A*Δx

Vediamo un'applicazione pratica

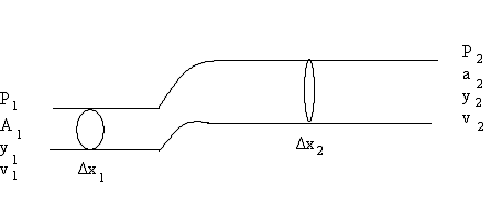
Le forze che agiscono sul sistema sono forze di pressione, di spinta e resistenza

P₁A₁Δx₁ P₂A₂Δx₂

forza di spostamento forza di resistenza

N.B.: A*Δx= ΔV

di conseguenza otterremo

L = P₁ΔV - P₂ΔV = ΔV (P₁-P₂)

Tornando all'equazione proposta inizialmente, modifichiamo i termini in maniera da ottenere un'equazione confrontabile con quella appena definita

ΔK = ½ *ς*ΔV (v²₁-v2₂) ς = ro = densità

ΔU = ς*ΔV*g (h₁-h₂)

L = ΔK - ΔU

P₁+1/2*ς*v²₁+ς*g*h₁ = P₂+1/2*ς*v²₂+ς*g*h₂

equazione di BERNOULLI

Ovvero la legge che regola la conservazione dell'energia meccanica x un fluido ideale incomprimibile

Possiamo avere formule semplificate dell'equazione base nei seguenti casi:

fluido fermo: P₁+ς*g*h₁ = P₂+ς*g*h₂

fluido fermo e orizzontale P₁= P₂

fluido in movimento orizzontale

P₁+1/2*ς*v²₁= P₂+1/2*ς*v²₂

P₁-P₂= ½* ς (v²₁-v²₂)

in questo caso particolare

se  A₁>A₂ v₁<v₂ P₁>P₂

A₁<A₂ v₁>v₂ P₁<P₂

es1

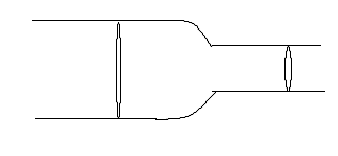
r₁=2cm

Q=10^-2m³/s

P=1,6*10⁵Pa

P₂=10⁵Pa

r₂=?

Q=A₁*v₁=A₂*v₂  utilizzo entrambe le equazioni in sistema

P₁+1/2ς*v₁²=P₂+1/2ς*v₂²

v₁= Q/A = 10^-2/πr² = 8m/s

_{___________________}

v₂ = √2/ς(P₁-P₂)+v₁² = 13,6m/s

_{_________}

A₂ = Q/v₂   π*r² = Q/v₂ r = √Q/v₂ π = 1,5cm

Principio di archimede

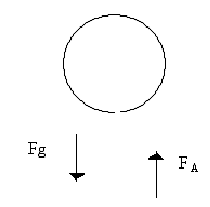
Il peso di un corpo di massa m viene percepito e misurato diversamente a seconda del mezzo (fluido) in cui è immerso

Questo perchè su di esso agiscono due forze di verso opposto:

Fg = la forza di gravità, con verso diretto al centro della terra

F_A= la spinta di archimede, con verso opposto a F_g e data dalla risultante delle pressioni parziali imposte sul corpo immerso dal fluido

La forza risultante, la quale determinerà come possibile o meno il galleggiamento del corpo sarà = a

F_R= -Fg+F_A

Per avere una formula + completa e utile, analizziamo le componenti delle forze

Fg = mg = ςc*V*g ς_c=densità corpo

ς_f=densità fluido

F_A = m₁g = ς_f*V₁*g

V e V₁, rispettivamente il volume del corpo e dell'acqua da esso spostata, solitamente sn valore coincidenti. Possono però essere differenti in alcuni casi particolari di galleggiamento in cui vi è soltanto una porzione del crpo sotto il livello del fluido. La parte rimanente, non essendo da esso toccata nn risente della spinta di archimede, e nn rientra quindi nella nostra equazione.

Dato che noi non misureremo la forza risultante, bensì la forza pesa che il corpo acquista nel fluido, questa sarà di modulo uguale ma segno opposto rispetto alla F_R

F_m= Fg-F_A

Assumendo che V sai uguale nei due casi

F_R = - ς _c*V*g + ς_F*V*g =

-V*g( ς _c- ς _F)

Analizzando i termini in parentesi, possiamo definire la risposta del corpo

ς_c-ς_F > 0 il corpo affonda

ς_c-ς_F < 0 il corpo galleggia

ς_c-ς_F = 0 il corpo rimane stazionario

Per i calcoli è possibile aiutarsi con la ς relativa, uguale al rapporto ς_c/ς_F

ς_rel = Fg/Fg-F_m  N.B. Fg-F_m= F_A

es: m=5kg

ς=7,8*10³kg/m³

F_m (peso nel fluido)= 6,16N

ς_F= ?

ς_rel = Fg/Fg-F_m = mg/mg-F_m = 1,14kg/m³

ς_F = ς_c/ς_F = 7,8*10³/1,14= 6,83kg/m³

es2:   ς_c = 200kg/m³ il corpo è in condizioni di galleggiamento stazionario sezionato dalla superficie

ς_F = 10³

V₁/V=?

Fg=F_A Fr= 0 -V(ς_c-ς_F) = 0 ςc*V*g = ς_F*V₁*g

V₁/V = ς_c/ς_F

Fluidi reali

In un fluido reale dobbiamo tenere conto, oltre alle normali foze applcate al liquido, dell'attrito, forza resistiva che interviene sia fra le molecole del fluido le une con le altre, sia tra queste e le pareti del recipiente/tubo in cui esse si trovano

Vmax v2 v3 v4 v5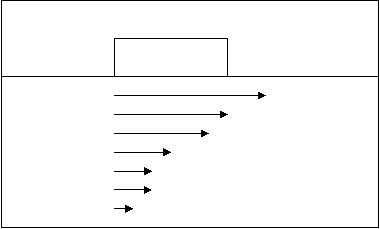

Si hanno velocità differenti per ogni ipotetica lamina di liquido, in quanto ognuna di esse è tanto più frenata dall'attrito quanto più si avvicina alle pareti del contenitore

I valori di queste velocità sono in buona parte influenzate dalla veocità; ora vedremo perchè:

Introduciamo il concetto di FORZA DI ATTRITO VISCOSO

Dipende da:

η: coefficiente di viscosità

profilo di velocità (da carattere essenzialmente parabolico, come vedremo in seguito

Δv/Δr = 2v_max/r  il coefficiente 2 è implicito xchè

in un tubo vi è metà inf.

Superficie di contatto

A_l =(2πr)l

di conseguenza

Fη = η* 2v_max/r*2πl*r

Fη = 4π*v_max*l

Si misura in Pioseuille (Pl)

Possiamo quindi ora definire le due forze, e compararle. Ciò è però possibile soltanto assumendo che la velocità sia costante. In questo caso la forza di spinta è uguale a quella frenante in quanto il fluido si muove per moto rettilineo uniforme.

ΔP*πr²

= 4πη*v_max*l

4η*v_max*l ΔP*r²

ΔP= ^{______________} e v_max= ^{_______________}

r² 4 η*l

Tornando al discorso della portata, in cui

Q = A*<v>

e tenendo conto del fatto che <v> (vel. Media) nn è altro che ½v_max

ΔP*r² πr⁴

Q = πr²*^__________ = ^_______ ΔP legge di HAGEN-POISEUILLE

8η*l 8η*l

Non è più possibile usare l'equazione di bernoulli in quanto la presenza di attrito viscoso non ci permette di considerare l'equazione di conservazione dell'energia, perchè una parte i questa viene dissipata.

Studiando l'equazione appena proposta possiamo notare che il rapporta tra pressione e portata, ci da quello che è stato definito come coefficiente di resistenza idraulica (R)

8η*l

ΔP/Q= ^_______ = R

πr⁴

N.B. Il raggio nelle due precedenti equaizoni è elevato alla quarta potenza. Di conseguenza una sua minima variazione implica importanti variazioni di R e Q.

Questa forzatura ha la sua spiegazione nel fatto che, così vista, la nostra equazione, può essere studiata in maniera del tutto analoga alla legge di ohm, che studia, invece di quella idraulica, la resistenza elettrica.

Andamento nei condotti

Grazie all'introduzione della resistenza ora possiamo studiare il comportamento dei fluidi reali all'interno di tubazioni che comportino variazioni di raggio in serie ed in parallelo (analogamente a quanto accade per le reti elettriche)

tubazioni in serie

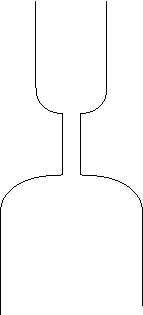
ΔP₁ Q₁ R₁

ΔP₂ Q₂ R₂

ΔP₃   Q₃ R₂

Nelle tubazioni poste in serie la portata non varia; a cambiare sarà la pressione, quindi

Q₁=Q₂=Q₃=Q

ΔP₁+ΔP₂+ΔP₃= Δp_tot

R_tot= ΔP/Q = ΔP₁/Q+ΔP₂/Q+ΔP₃/Q= R₁₊R₂₊R₃

tubazioni in parallelo

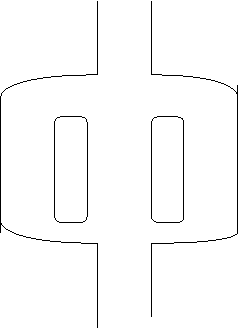
R₁ R₂ R₃

ΔP_tot= ΔP₁=ΔP₂=ΔP₃

Q_tot= Q₁+Q₂+Q₃

Q_tot= ΔP/R_tot = ΔP/R₁+ΔP/R₂+ΔP/R₃

1/R_tot =1/R₁+1/R₂+1/R₃

Quanto postulato fin'ora in base all'asserzione che il moto delfluido sia un moto laminare = in ogni suo punto.

Questo vale a basse velocità. A velocità elevate, si viene a formare un moto TURBOLENTO, nn più laminare.

MOTO TURBOLENTO 12/10/06

Questo moto prende il nome dalle turbolenze verticali che vengono a formarsi in un fluido in moto orizzontale

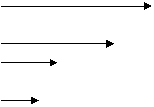
moto laminare moto turbolento

Quando questo moto caraterizza solo una piccola parte del condotto, si vengono a formare dei vortici, che trascnano con loro altre particelle aumentando ulteriormente la dissipazione dell'energia prodotta dal moto turbolento

Registriamo perdite dei seguenti tipi

dissipazione

diminuzione del tragitto percorso dalle particelle

trasferimento energetico alle altre molecole

Dato che il moto nn è più laminare nn è più possibile usare la legge di hagel-poiseuille

Bisogna comunque dire che molte volte questo moto presenta caratteristiche positive

rimescolamento sanguigno

rimescolamento dei carburanti durante l'iniezione

formazioni di rumore di fondo durante la compressione di vasi sanguigni, utile per la misura della pressione

Serve pote misurare un limite al di sopra del quale un moto possa essere considerato turbolento per poter usare le giuste leggi nel giusto caso.

DETERMINAZIONE DEL LIMITE (N. DI REYNOLDS)

Cerchiamo un numero adimensionale il cui valore dipenda dalle varirabili caratteristiche dei fluidi e indichi il tipo di moto proprio di quel fluido in quelle condizione.

Dovrà dipendere da:

v = m/s

r = m

ρ=kg/m₃

η=N*s/m

Questo coefficiente, detto numero di Reynolds sarà pari a

R_e= r*ρ*<v> >1000 moto sicuramente turbolento

^___________ >1000 moto probabilmente laminare

η

Quando abbiamo a che fare con un moto turbolento nn ci è possibile, data la velocità media, risalire a quella massima, datala decaduta della legge di HAGEL.

In questi casi il moto della singola particelle è imprevedibile

TENSIONE SUPERFICIALE

La particella ha interazioni con tutte le particelle che la circondano; tutte le forze si bilanciano perfettamente

in questo caso (molecola superficiale), le forze nn sono perfettamente bilanciate; per questo la loro risultante è diretta verso l'interno

La tensione superficiale definisce la tendenza delle molecole superficiale di stare legate le une alle altre.

Questo determina, per esempio, la forma sferica delle gocce d'acqua, forma con superficie relativa inferiore a tutte le altre.