Bertrand Russel died in 1970.
The
Prologue to Bertrand Russell's Autobiography
What I Have Lived For
Three passions, simple but
overwhelmingly strong, have governed my life: the longing for love, the search
for knowledge, and unbearable pity for the suffering of mankind. These
passions, like great winds, have blown me hither and thither, in a wayward
course, over a great ocean of anguish, reaching to the very verge of despair.
I have sought love, first, because it brings ecstasy -
ecstasy so great that I would often have sacrificed all the rest of life for a
few hours of this joy. I have sought it, next, because it relieves
loneliness--that terrible loneliness in which one shivering consciousness looks
over the rim of the world into the cold unfathomable lifeless abyss. I have
sought it finally, because in the union of love I have seen, in a mystic
miniature, the prefiguring vision of the heaven that saints and poets have
imagined. This is what I sought, and though it might seem too good for human
life, this is what--at last--I have found.
With equal passion I have sought knowledge. I have
wished to understand the hearts of men. I have wished to know why the stars
shine. And I have tried to apprehend the Pythagorean power by which number
holds sway above the flux. A little of this, but not much, I have achieved.
Love and knowledge, so far as they were possible, led
upward toward the heavens. But always pity brought me back to earth. Echoes of
cries of pain reverberate in my heart. Children in famine, victims tortured by
oppressors, helpless old people a burden to their sons, and the whole world of
loneliness, poverty, and pain make a mockery of what human life should be. I
long to alleviate this evil, but I cannot, and I too suffer.
This has been my life. I have found it worth living,
and would gladly live it again if the chance were offered me.
Russell's
Paradox
Russell's paradox is the most
famous of the logical or set-theoretical paradoxes. The paradox arises within
naive set theory by considering the set of all sets that are not members of
themselves. Such a set appears to be a member of itself if and only if it is
not a member of itself, hence the paradox.
Some sets, such as the set of all teacups, are not
members of themselves. Other sets, such as the set of all non-teacups, are
members of themselves. Call the set of all sets that are not members of
themselves S. If S is a member of itself, then by
definition it must not be a member of itself. Similarly, if S is not a member of itself, then by
definition it must be a member of itself. Discovered by Bertrand Russell in 1901, the
paradox prompted much work in logic, set theory and the philosophy and
foundations of mathematics during the early part of the twentieth century.
History of the
paradox
Russell discovered his
paradox in May of 1901 while working on his Principles of Mathematics (1903). Cesare Burali-Forti, an
assistant to Giuseppe Peano, had discovered a similar antinomy in 1897 when he
noticed that since the set of ordinals is well-ordered, it, too, must have an
ordinal. However, this ordinal must be both an element of the set of ordinals
and yet greater than any such element.
Russell wrote to Gottlob Frege with news of his
paradox on June 16, 1902. The paradox was of significance to Frege's logical
work since, in effect, it showed that the axioms Frege was using to formalize
his logic were inconsistent. Specifically, Frege's Rule V, which states that
two sets are equal if and only if their corresponding functions coincide in
values for all possible arguments, requires that an expression such as f(x) may be considered to be both a
function of the argument f and
a function of the argument x.
In effect, it was this ambiguity that allowed Russell to construct S in such a way that it could be a member
of itself.
Russell's letter arrived just as the second volume of
Frege's Grundgesetze der Arithmetik
(The Basic Laws of Arithmetic,
1893, 1903) was in press. Immediately appreciating the difficulty that the
paradox posed, Frege hastily added an appendix to the Grundgesetze which discussed Russell's discovery.
Nevertheless, he eventually felt forced to abandon many of his views as a
result of the paradox. Russell himself first discusses the paradox in detail in
an appendix to his Principles of
Mathematics.
Significance of the paradox
The significance of Russell's
paradox can be seen once it is realized that, using classical logic, all
sentences follow from a contradiction. (For example, assuming both P and ~P,
we can prove any arbitrary Q as
follows: from P we can obtain P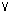 
Q by the rule of
Addition, and then from P Q and ~P we can obtain Q by the rule of Disjunctive Syllogism.)
In the eyes of many, it therefore appeared that no mathematical proof could be
trusted if it was discovered that the logic and set theory apparently
underlying all of mathematics was contradictory.
Russell's paradox stems from the idea that any
coherent condition may be used to determine a set. Attempts at resolving the
paradox therefore have typically concentrated on various means of restricting
the principles governing the existence of sets. Naive set theory contained the
so-called unrestricted comprehension (or abstraction) axiom. This is an axiom,
first introduced by Georg Cantor, to the effect that any predicate expression, P(x), containing x as a free variable will determine a
set. The set's members will be exactly those objects that satisfy P(x), namely every x that is P. It is now generally agreed that such an axiom must be
either abandoned or modified.
Russell's response to the paradox is contained in his
theory of types. His basic idea is that we can avoid reference to S (the set of all sets that are not
members of themselves) by arranging all sentences into a hierarchy. This
hierarchy will consist of sentences (at the lowest level) about individuals,
sentences (at the next lowest level) about sets of individuals, sentences (at
the next lowest level) about sets of sets of individuals, etc. It is then
possible to refer to all objects for which a given condition (or predicate)
holds only if they are all at the same level or of the same "type".
Although Russell first introduced the idea of types in his Principles of Mathematics, the theory
found its mature expression five years later in his 1908 article
"Mathematical Logic as Based on the Theory of Types" and in the
monumental work he co-authored with Alfred North Whitehead, Principia Mathematica (1910, 1912,
1913). In its details, Russell's type theory thus came to admit of two
versions, the "simple theory" and the "ramified theory".
Both versions have been criticized for being too ad hoc to eliminate the
paradox successfully.
Other responses to the paradox include those of David
Hilbert and the formalists (whose basic idea was to allow the use of only
finite, well-defined and constructible objects, together with rules of
inference that were deemed to be absolutely certain), and of Luitzen Brouwer
and the intuitionists (whose basic idea was that one cannot assert the
existence of a mathematical object unless one can also indicate how to go about
constructing it).
Yet a fourth response to the paradox was Ernst
Zermelo's 1908 axiomatization of set theory. Zermelo's axioms were designed to
resolve Russell's paradox by restricting Cantor's naive comprehension
principle. ZF, the axiomatization generally used today, is a modification of Zermelo's
theory developed primarily by Abraham Fraenkel.
These four responses to the paradox have helped
logicians develop an explicit awareness of the nature of formal systems and of
the kinds of metalogical results that are today commonly associated with them.
He
achieved only a little of it
|
|
Pity
brought him back to heart
|
|
Love
and knowledge led him upward toward the heavens
|
|
- Children in famine
- Victim tortured by
oppressors
- Helpless old people
|
|
- It brings ectasy
- It relieves lonelines
- It prefigures the heaven
|
|
- The hearts of man
- Why the stars shine
- The Pythagorean power of
number
|
|
Pity for the suffering of mankind
|
|
Was
governed by three passions:
|
|
THIS WAS IS LIFE AND HE FOUND IT WORTH
LIVING
Bertrand Russell (1872-1970 ) was born in Trelleck, Wales. His parents died when he was
three years old. He was educated privately and went to Trinity College, Cambridge,
where he was a brilliant student of mathematics and philosophy. In 1900,
Russell became acquainted with the work of the Italian mathematician Peano,
which inspired him to write The Principles of Mathematics (1903),
expanded in collaboration with Alfred No 515f59f rth Whitehead into three volumes of Principia
Mathematica (1910-13). The research, which Russell did during this period
together with Whitehead and which is preserved in many books and essays,
establishes him as one of the founding fathers of modern analytical philosophy.
Throughout his life Russell has also been an extremely outspoken and aggressive
moralist in the rationalist tradition of Locke and Hume. His many essays, often
in the form of short reflections or observations on moral or psychological
topics, are written in a terse, vivid, and provocative style. His greatest
literary achievement has been his History of Western Philosophy (1946). 
