Il parsec e la parallasse

Il parsec (pc), abbreviazione di parallasse-secondo, è la distanza alla quale il raggio medio dell'orbita terrestre verrebbe visto sotto l'angolo di un secondo di grado.

1 parsec corrisponde a 3,26 anni-luce e a 206.265 UA.

Tale unità di misura deriva dal fatto che le prime misure di distanza in astronomia, effettuate per le stelle più vicine, si basavano su metodi trigonometrici, tramite determinazione dell'angolo di parallasse.

Il termine parallasse indica lo spostamento apparente di due punti situati a distanza diversa dall'osservatore quando quest'ultimo si sposta lungo una retta trasversale alla linea di osservazione.

E' il medesimo effetto prospettico che si produce quando, osservando un dito proteso davanti a noi, prima con il solo occhio destro e poi con il solo occhio sinistro, esso sembra muoversi rispetto allo sfondo.

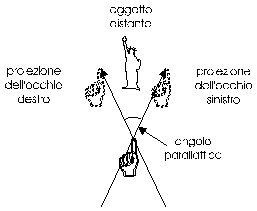
La distanza tra i due punti di osservazione è detta base parallattica. Nel caso dell'esempio precedente la base parallattica è costituita dalla distanza interoculare. Le due proiezioni che si ottengono saranno evidentemente tanto più separate quanto maggiore è la base parallattica e/o quanto più vicino è l'oggetto all'osservatore. L'angolo compreso tra le due visuali è detto angolo parallattico o parallasse.

Per ottenere uno spostamento parallattico di un pianeta rispetto allo sfondo delle stelle fisse è necessaria una base parallattica sufficientemente estesa, ad esempio il diametro terrestre.  Per utilizzare il diametro terrestre come base parallattica è sufficiente eseguire 2 osservazioni a distanza di 12 ore, aspettando che la terra compia mezzo giro intorno al suo asse. La metà dell'angolo compreso tra le due visuali è detto parallasse diurna.

Per poter ottenere effetti parallattici per oggetti più distanti dei pianeti (come sono appunto le stelle) è necessario prendere come base parallattica l'asse maggiore dell'orbita terrestre, eseguendo le osservazioni a distanza di 6 mesi. In 12 mesi le stelle più vicine sembrano infatti percorrere un ellisse sullo sfondo delle stelle più lontane (fisse). Tale ellisse non è altro che la proiezione dell'orbita della terra sulla sfera celeste. L'angolo 2 sotto il quale noi osserviamo l'asse maggiore di tale ellisse apparente è lo stesso sotto cui un osservatore posto sulla stella osserverebbe l'asse maggiore dell'orbita terrestre. La metà di tale angolo, pari ad , è detto parallasse annua della stella. Tale angolo permette la misura della distanza d della stella (o del pianeta in caso di parallasse diurna). Ricordando infatti che in un triangolo rettangolo il rapporto tra le misure dei cateti è pari alla tangente dell'angolo opposto al primo cateto, potremo scrivere:

Naturalmente lo spostamento apparente e il conseguente valore della parallasse risulterà tanto maggiore quanto più la stella è vicina alla terra, mentre diminuirà, al punto da non essere più misurabile per stelle molto distanti. Quando la parallasse annua di una stella è di 1" (1/3600 di grado), la relazione precedente fornisce una distanza di

Una stella dista quindi 1 parsec dalla terra quando misuriamo per essa un angolo di parallasse di 1 secondo di grado (1"). Nessuna stella, per quanto vicina, presenta una parallasse superiore al secondo di grado. La stella più vicina, Proxima Centauri (cielo australe), presenta una parallasse di 0,76" e quindi dista da noi 3,26/0,76 = 4,3 al. Le prime determinazioni di una parallasse stellare annua si devono a Struve (1822 - Aquilae 0,181") e a  Bessel (1837 - 31 Cygni 0,314").

È facile verificare che la distanza della stella, espressa in parsec è inversamente proporzionale all'angolo di parallasse. Se p è la parallasse annua, allora

Se misuriamo un angolo di mezzo secondo di grado la stella si trova ad una distanza doppia (2 pc), se misuriamo un angolo di 1/10 di secondo la distanza è dieci volte maggiore (10 pc) e così via.  Attualmente i nostri strumenti non ci permettono di apprezzare angoli inferiori al centesimo di secondo ed è quindi impossibile determinare la parallasse di stelle la cui distanza sia superiore a 100 parsec (circa 300 al).

Immaginiamo che l'orbita terrestre giaccia su di una circonferenza che abbia come centro la stella di cui vogliamo misurare la distanza d.

Poiché le parallassi stellari presentano, come abbiamo appena visto, valori molto piccoli, sempre inferiori al secondo di grado, possiamo ragionevolmente confondere l'arco TT₁ con la corda ad esso sottesa, la quale rappresenta il diametro dell'orbita terrestre. Ricordando che un radiante è l'angolo che sottende un arco lungo quanto il raggio della circonferenza, potremo scrivere la seguente proporzione

1 rad : d = a : 1 UA

Poiché ovviamente in una circonferenza sono contenuti 2p radianti pari a 360°, un radiante corrisponde a 360°/2p = 57,29578 ° = 206.264,8 ". Se dunque esprimiamo gli angoli in secondi di grado, la proporzione precedente diventa 206.264,8 : d = a : 1 UA  e la distanza d della stella, espressa ovviamente in UA, varrà .

Ma essendo 1 pc = 206.264,8 UA, la distanza in parsec è pari a