|
|
| |
Un
capannone industriale, avente le dimensioni in pianta di 33,16 x
1. PROGETTO E CALCOLO DEI VARI ELEMENTI STRUTTURALI.
La struttura viene progettata con pilastri in acciaio serie HE, nei quali vengono vincolate a cerniera le capriate realizzate con profilati a L con lati e collegamenti bullonati. Le terzere di collegamento fra le capriate vengono eseguite con profilati HE posizionati in corrispondenza dei nodi, sulle quali viene posata la copertura in lamiera ondulata a doppio strato coibentato. In corrispondenza delle ultime campate laterali delle terzere e a livello verticale nelle campate prima, ultima e centrale verranno realizzate le diagonali di controventatura.
2. CALCOLO DELLE TERZERE. 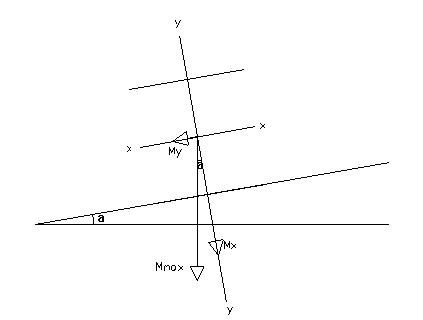
2.1. Analisi dei carichi (in proiezione orizzontate).
Carico d'esercizio (neve + vento) =1,50 KN/ m²
Lamiera ondulata a doppio strato coibentato =0,40 KN/m²
Peso proprio terzere HE 120 B ![]() =
=![]() =0,14 KN/m²
=0,14 KN/m²
![]() ²
²
L'inclinazione è α = 10°
Lo schema statico di ogni terzera corrisponde a quello di una trave appoggiata alla estremità su due capriate consecutive, gravata da un carico ripartito di inte 838g67i nsità;
q = 2,04 Kn/m2 x 1,904 = 3,88 KN/m.
Per effetto dell'inclinazione, l'asse di sollecitazione non coincide con uno degli assi principali d'inerzia e pertanto la terzera è sollecitata a flessione deviata, il momento flettente massimo che agisce nel piano verticale risulta:
Mmax = ![]() x q x l² =
x q x l² = ![]() x 3,88 x 5,50² = 14,67 KN m
x 3,88 x 5,50² = 14,67 KN m
Il quale viene scomposto ottenendo i momenti nei piani aventi come traccia gli assi principali x e y della sezione:
Mx = Mmax x cos = 14,67 x cos10° = 14,45 KN m
My = Mmax x sen = 14,67 x sen10° =2,55 KN m
2.2. Progetto della sezione.
Assumendo il coefficiente
c = ![]() = 2,75
= 2,75
per sezioni sino a circa h=140mm
si ha:
W = ![]() =
= ![]() = 94,69 cm
= 94,69 cm
Dalle tabelle si rileva la necessità di impiegare un profilo HE 120 B con:
Wx=
144cm³; Wy= 53cm³; Ix= 864cm![]() ; Iy= 318cm
; Iy= 318cm![]()
2.3. Verifica a flessione deviata.
![]() +
+ ![]() =
= ![]() +
+ ![]() = 14864,04 N/mm
= 14864,04 N/mm
148,46 N/cm < 160N/cm
2.4. Verifica a deformazione.
La freccia totale si può ottenere componendo la freccia fx per l'inflessione nel piano avente per traccia l'asse y con quella fy che si ha per l'inflessione nel piano con traccia l'asse x; è peraltro necessario scomporre il carico q secondo le direzioni dei suddetti assi:
qx = q x cos 3,88 x cos10° = 3,82 Kn/m= 38,20 N/cm
qy = q x sen = 3,88 x sen10° = 0,67Kn/m = 6,70N/cm
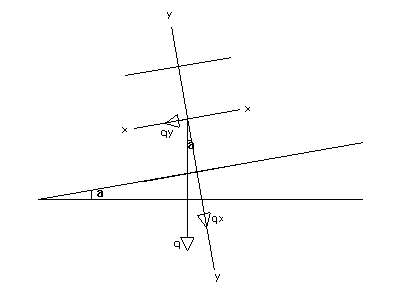
Si ha quindi:
fx =![]() x
x ![]() =
= ![]() x
x ![]() = 2,51cm
= 2,51cm
fy = ![]() x
x ![]() =
= ![]() x
x ![]() = 1,19cm
= 1,19cm
ftot = f![]() + f
+ f![]() = fx x cos + fy x sen = 2,51 x cos10° + 1,19 x sen10° = 2,68cm
= fx x cos + fy x sen = 2,51 x cos10° + 1,19 x sen10° = 2,68cm
valore inferiore alla freccia massima ammissibile che per elementi ci copertura risulta:
famm = ![]() x l =
x l = ![]() x 550 = 2,75cm
x 550 = 2,75cm
2.5. Verifica a taglio.
La verifica viene effettuata solo per la componente dello sforzo di taglio con intensità maggiore dovuta al carico qx; applicando la formula approssimata si ha:
m = ![]() =
= ![]() =
= 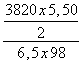 = 16,49 N/mm < adm
= 16,49 N/mm < adm
adm = 0,577 x adm = 0,577 x 160 = 92,32 N/mm
2.6. Reazioni vincolari.
P = q x ic x it = 2,04 x 5,50 x 1,904 = 21,36 KN
Va = Vb = ![]() =
= ![]() = 96,12 KN
= 96,12 KN
3. CALCOLO DELLA CAPRIATA.
Il calcolo della capriata viene effettuato utilizzando il Metodo Cremoniano ottenendo gli sforzi compiuti dalle rispettive aste:
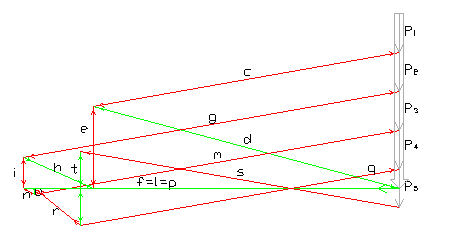
|
Aste |
Puntoni |
Tiranti |
|
a |
|
|
|
b |
|
|
|
c |
|
|
|
d |
|
|
|
e |
|
|
|
f |
|
|
|
g |
|
|
|
h |
|
|
|
i |
|
|
|
l |
|
|
|
m |
|
|
|
n |
|
|
|
o |
|
|
|
p |
|
|
|
q |
|
|
|
r |
|
|
|
s |
|
|
|
t |
|
|
Scala distanze 1cm = 1m
Scala forze 1cm = 1KN
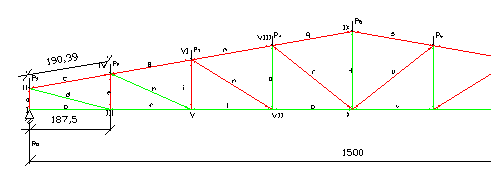
3.1.1. Metodo di Ritter per verificare lo sforzo dell'asta d
Ra x xa - P1 x x1- Sd x xd = 0
96,12 x 2,84 - 21,36 x 2,84 - Sd x 1,215 = 0
Sd = ![]() = 174,75 KN
= 174,75 KN
3.1.2 Metodo di Ritter per verificare lo sforzo dell'asta e
Ra x xa - P1 x x1- Se x xe = 0
96,12 x 2,84 - 21,36 x 2,84 - Se x 4,71 = 0
Se = ![]() = 45,08 KN
= 45,08 KN
3.1.3 Metodo di Ritter per verificare lo sforzo dell'asta g
Ra x xa - P1 x x1- P2 x x2 - Sg x xg = 0
96,12 x 3,75 - 21,36 x 3,75 - 21,36 x 1,875 - Sg x 1,16 = 0
Sg = ![]() = 206,76 KN
= 206,76 KN
3.1.4 Metodo di Ritter per verificare lo sforzo dell'asta l
Ra x xa - P1 x x1- P2 x x2 - Sl x xl = 0
96,12 x 3,75 - 21,36 x 3,75 - 21,36 x 1,875 - Sg x 1,16 = 0
Sl = ![]() = 206,76 KN
= 206,76 KN
3.2. Calcolo di progetto delle aste.
3.2.1. ASTA D (saettone)
Questa asta è soggetta a compressione e viene realizzata con una sezione composta costituita da due angolari a lati uguali ed è dimensionata in funzione dello sforzo massimo:
Sd = 174,75 KN = 174750N
A = ![]() =
= ![]() = 10,92 cm²
= 10,92 cm²
Si impiega una sezione costituita da due angolari con lati uguali 45x45x7 disposti a T con A=11,7 cm²
ASTA E (monaco)
A differenza della precedente questa asta è soggetta a trazione con uno sforzo massimo:
Se = 45,08 KN = 45080 N
Per il predimensionamento adotteremo una σadm ridotta pari a 11500 N/cm². Le aste vengono realizzate con una sezione composta costituita da due angolari ad ali uguali applicati a T:
A = ![]() =
= ![]() = 3,92 cm²
= 3,92 cm²
L'asta ha una lunghezza:
l = 0,50 + (sen10° x 1,875) =
e viene realizzata con due angolari ad ali uguali 35x35x4 con le seguenti caratteristiche:
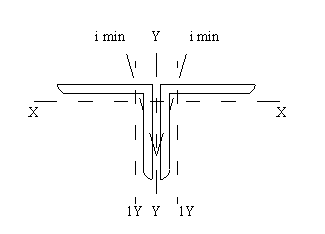
A = 5 ,34 cm²; ix = i min = ![]() min =
min =
I due angolari vengono collegati con imbottiture disposte ad interasse:
l![]() = l x β = 0,83 x 1 =
= l x β = 0,83 x 1 =
L![]() =
= ![]() =
= ![]() =
= ![]() 50 x i
50 x i![]() min =
min =
La sezione appartiene al gruppo II per cui la snellezza equivalente risulta:
λ![]() =
= ![]() =
= 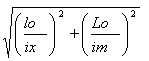 =
= 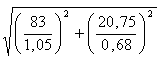 =
=
La snellezza del singolo profilato vale:
λy = ![]() =
= ![]() = 47,43
= 47,43 ![]() λ
λ![]()
Quindi il
coefficiente ω viene ricavato in funzione della λ![]() e risulta pari a 1,715.
e risulta pari a 1,715.
La tensione massima è:
= ![]() =
= ![]() = 14477,94 N/cm² = 144,78 N/mm²
= 14477,94 N/cm² = 144,78 N/mm² ![]() σadm
σadm
Viene ancora
effettuata la verifica del profilato singolo compreso fra due imbottiture
successive, per cui risulta L![]() =
=
λ = ![]() =
= ![]() = 30,51 = 31
= 30,51 = 31
Valore al quale corrisponde ω = 1,067 per cui si ha:
![]() =
= 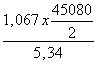 = 4503,78 N/cm² = 45,04 N/mm²
= 4503,78 N/cm² = 45,04 N/mm²![]() σadm
σadm
ASTA G (montante)
Come la precedente anche questa asta è soggetta a trazione con uno sforzo massimo:
Sg = 210,13 KN = 210130 N
Come nel caso precedente per il predimensionamento adotteremo una σadm ridotta pari a 11500 N/cm². Le aste vengono realizzate con una sezione composta costituita da due angolari ad ali uguali applicati a T:
A = ![]() =
= ![]() = 17,51 cm²
= 17,51 cm²
L'asta ha una lunghezza:
l = ![]() =
=
e viene realizzata con due angolari ad ali uguali 70 x 70 x 11 con le seguenti caratteristiche:
A = 28,6 cm²; ix = i min = ![]() min =
min =
I due angolari vengono collegati con imbottiture disposte ad interasse:
l![]() = l x β = 1,904 x 1 =
= l x β = 1,904 x 1 =
L![]() =
= ![]() =
= ![]() =
= ![]() 50 x i
50 x i![]() min =
min =
La sezione appartiene al gruppo II per cui la snellezza equivalente risulta:
λ![]() =
= ![]() =
= 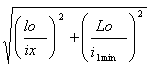 =
= 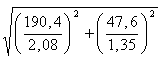 =
=
La snellezza del singolo profilato vale:
λy = ![]() =
= ![]() = 58,22
= 58,22![]() λ
λ![]()
Quindi il
coefficiente ω viene ricavato in funzione della λ![]() e risulta pari a 1,99 . La tensione massima è:
e risulta pari a 1,99 . La tensione massima è:
![]() =
= ![]() = 14633,46 N/cm² = 146,33 N/mm²
= 14633,46 N/cm² = 146,33 N/mm² ![]() σadm
σadm
Viene ancora
effettuata la verifica del profilato singolo compreso fra due imbottiture
successive, per cui risulta L![]() =
=
λ = ![]() =
= ![]() = 35,26 = 36
= 35,26 = 36
Valore al quale
corrisponde ω = 1,102 per cui si ha:![]()
![]() =
= 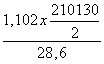 = 4051,77 N/cm² = 40,52 N/mm²
= 4051,77 N/cm² = 40,52 N/mm²![]() σadm
σadm
3.2.4. ASTA L (catena)
Questa asta è soggetta a compressione e viene realizzata con il medesimo tipo di sezione composta delle aste precedenti ed è calcolata in funzione dello sforzo massimo:
Sl = 206,93 KN = 206930N
A = ![]() =
= ![]() = 12,93 cm²
= 12,93 cm²
Si impiega una sezione costituita da due angolari con lati uguali 60 x 60 x 6 disposti a T con A = 13,8 cm².
4. CALCOLO DEL PESO PROPRIO DELLA CAPRIATA.
MONTANTI
Asta c + Asta g + Asta m + Asta q = 0,112 x 2 x 7,62 x 2 = 3,414 KN
CATENA
Asta b + Asta f + Asta l + Asta p = 0,0542 x 2 x 15 = 1,626 KN
MONACI
Asta a = 0,0242 x 2 x 0,50 = 0,0242 KN
Asta e = 0,0242 x 2 x 0,83 = 0,0402 KN
Asta i = 0,0242 x 2 x 1,16 = 0,0562 KN
Asta o = 0,0242 x 2 x 1,49 = 0,0722 KN
Asta t = 0,0242 x 2 x 1,802 = 0,04882 KN
Tot monaci = 0,4738 KN
SAETTONI
Asta d = 0,0495 x 2 x 1,94 = 0,192 KN
Asta h = 0,0495 x 2 x 2,05 = 0,203 KN
Asta n = 0,0495 x 2 x 2,21 = 0,218 KN
Asta r = 0,0495 x 2 x 2,39 = 0,237 KN
Tot saettoni = 1,7002 KN
TOTALE CAPRIATA = 7,214 KN
5. CALCOLO DEL PILASTRO IN ACCIAIO.
5.1. Analisi dei carichi.
Peso Proprio Capriata
![]() = 99,73 KN
= 99,73 KN
Peso proprio presunto dei fazzoletti e dei collegamenti
![]() =
0,90 KN
=
0,90 KN
Peso proprio presunto pilastro HE 160 B
0,426 x 6,50 =2,80 KN
![]()
Per le eventuali controventature si adotta P = 105 KN. Si fissa ad arbitrio una snellezza λ = 150 e dalle tabelle si ricava ω = 3,46 per cui la sezione resistente risulta:
A = ![]() =
= ![]() = 22,71 cm²
= 22,71 cm²
La lunghezza libera di inflessione viene calcolata con β = 1 perché i vincoli dell'asta possono assimilarsi a cerniere:
lo =
6,50 x β = 6,50 x 1 =
utilizzeremo un profilato HE 160 B con raggio d'inerzia minimo imin = 4,05 che fornisce una snellezza reale:
![]() =
= ![]() = 160,49 = 161
= 160,49 = 161
Con il valore di ω = 3.893 reale si procede alla verifica:
![]() =
= ![]() = 7527,90
N/cm² = 75,28 N/mm²<160 N/mm²
= 7527,90
N/cm² = 75,28 N/mm²<160 N/mm²
6. CALCOLO DELLA PIASTRA DI BASE.
Il plinto di fondazione verrà realizzato con calcestruzzo di classe 25 con una tensione ammissibile a compressione:
![]() = 0,7
x
= 0,7
x ![]() = 0,7 x
= 0,7 x ![]() = 5,95 N/mm
= 5,95 N/mm
La piastra di ancoraggio sarà
realizzata con acciaio Fe 510 con tensione ammissibile ![]() e verrà ancorata al
plinto mediante due bulloni con diametro
e verrà ancorata al
plinto mediante due bulloni con diametro
la = lb = 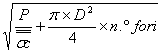
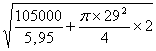
Essendo tale valore troppo piccolo si utilizzerà una
piastra con la = lb =
6.1. Calcolo dello spessore della piastra.
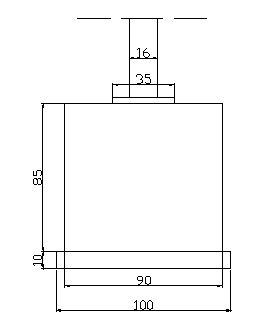
Lo spessore (t) viene determinato ipotizzando che il carico P trasmesso dal pilastro si ripartisca su una superfici fittizia con lati:
h' = 0,90 x h = 0,90 x 160 =
b' = 0,80 x h = 0,80 x 160 =
h e b sono la base e l'altezza del pilastro HE 160 B. La piastra presenta due mensole di lati uguali e fra loro ortogonali con luci:
m = ![]() =
= ![]() =
=
n = ![]() =
= ![]() =
=
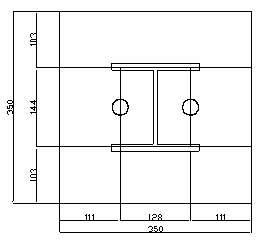
Delle due luci si assume quella maggiore
quindi n =
La pressione di contatto tra piastra e fondazione vale:
![]()
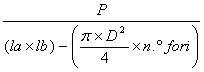 =
= 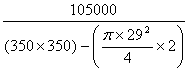 = 0,86N/mm
= 0,86N/mm
È perciò necessaria una piastra con spessore:
t = ![]() =
= ![]() =
=
Per la rigidezza lo spessore viene
portato a
7. PROGETTO FONDAZIONE (PLINTO MASSICCIO).
7.1. Analisi dei carichi.
Carico trasmesso dal pilastro = 105 KN
Peso proprio piastra
(0,03 x0,03 x 0,35) x 78,5 KN/m![]() = 0,29 KN
= 0,29 KN
![]()
Il peso proprio presunto del plinto, per il dimensionamento si assume pari a circa un decimo di quello gravante sull' opera di fondazione, pertanto si ha:
G = ![]() x P =
x P = ![]() x 105,29 =
10,53 KN
x 105,29 =
10,53 KN
Il carico totale sul terreno risulta pari a:
F = G + P = 10,53 + 105,29 = 115,82 KN
L'area di base del plinto è quindi:
A = ![]() =
= ![]() = 7238,75 cm²
= 7238,75 cm²
La sezione si assume quadrata come quella del pilastro con lato di:
l = ![]() =
= ![]() =
=
Adotteremo un plinto di fondazione
quadrato con lato di
![]() = 0,4 +
= 0,4 + ![]() = 0,4 +
= 0,4 + ![]() = 0,53 N/mm²
= 0,53 N/mm²
Affinché non abbia punzonamento l'altezza del plinto deve essere:
h = ![]() =
= ![]() =
=
Mentre considerando il prisma di scarico l'altezza risulta:
h = c x tan ![]() x tan60° =
x tan60° =
L'altezza si assume pari a
G' = [(1,00 x
1,00 x 0,10) x 24 KN/m![]() + (0,90 x 0,90 x 0,80) x 24
KN/m
+ (0,90 x 0,90 x 0,80) x 24
KN/m![]()
= 2,4 + 15,55 = 17,95 KN
Per cui il carico totale sul terreno risulta:
F' = P + G' = 105 + 17,95 = 122,95KN
Essendo il carico centrato la tensione sul terreno è uniforme e vale:
![]() =
= ![]() =
= ![]() = 15,18 KN/cm²
= 15,18 KN/cm² ![]() 16 KN/cm²
16 KN/cm²
Al di sotto della struttura plinto e sottoplinto si dispone una rete elettrosaldata del Ø 12 per stabilizzare ulteriormente il piano d'appoggio.
![]()
|
Privacy |
Articolo informazione
Commentare questo articolo:Non sei registratoDevi essere registrato per commentare ISCRIVITI |
Copiare il codice nella pagina web del tuo sito. |
Copyright InfTub.com 2024